FIRST HALF
 It's December 25. It's held at the Olympic Stadium in Montreal a benefit match in favor of the Misunderstood Mathematicians.
It's December 25. It's held at the Olympic Stadium in Montreal a benefit match in favor of the Misunderstood Mathematicians.
The initial line-up of one team consists of the following players:
| Player | Age |
|---|---|
| Manuel Neuer | 26 |
| Thomas Vermaelen | 27 |
| Daniel Agger | 28 |
| Fabio Coentrao | 24 |
| Yaroslav Rakitskiy | 23 |
| Jesús Navas | 27 |
| Samir Nasri | 25 |
| Urby Emanuelson | 26 |
| Theo Walcott | 23 |
| Mario Balotelli | 22 |
| Robert Lewandowski | 24 |

The mean age of the team is exactly 25 years.
In minute 60, the coach decides to replace Nasri (25 years) by another player.
After the substitution, the average age has risen 2 years.
Could you estimate how old is the new player?
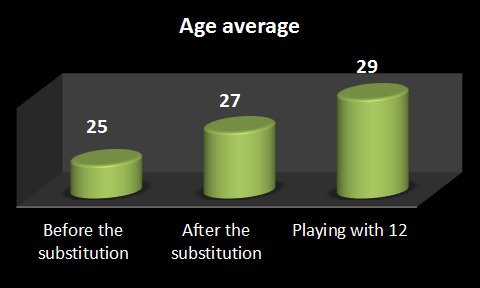
After this change, the coaches of both teams decide to play the last quarter of hour with 12 players.
How old should be the new player entering, to re-up the average another 2 years?
Go to the second half to discover the solution

SECOND HALF
In the first case, for calculating the age of the player chosen to enter the pitch to increase the average age two years, the easiest method is as follows.
We will add the years of all the players. If the average age is 25 years, and there are 11 players, we multiply: 25 * 11 = 275.
After replacement, the players will total: 27 * 11 = 297 years.
As there is a difference of 297 - 275 = 22 years, this means that the reserve must have 22 years more than the substituted player, in this case: 22 + 25 = 47 years
 A nice Christmas gift to Gheorghe Hagi!
A nice Christmas gift to Gheorghe Hagi!
In case there are 12 players on the pitch, the calculations would be as follows. Total years before substitution: 27 * 11 = 297
Total years after the change: 29 * 12 = 348. Unlike years: 348 - 297 = 51 years. The incoming player must be 51 years old.
 Another Christmas gift, now to Lothar Matthäus!
Another Christmas gift, now to Lothar Matthäus!
Sometimes when we walk into a room where, for example, is held a competition of ballroom dancing for over 80 years, or a competition of games consoles for under 10, we use to say: 'I've just pushed up / down the average age 5 years'.
Actually, we control the concept of average in a relatively correct way when it comes to handling a few values, but we start to lose the global view of the average as we increase the population we study.
Thus, if we consider the second case, let's see what we need to modify the mean age of a group in a year, when we add another element to the group.
If we call x1,x2,...xn to the different ages of the people from a group of n individuals, their mean age will be:
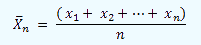
If we now add one more person (n+1), the average age should be:
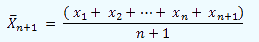
If we want this average varies in a 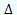 number of years respect to the previous average, we'll have:
number of years respect to the previous average, we'll have:
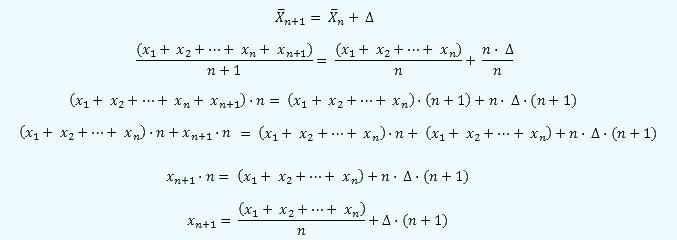
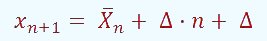
So each year (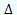 = 1) we want to increase the age mean of a population, we need to introduce a person with an age equal to the previous average age plus the total number of individuals plus 1.
= 1) we want to increase the age mean of a population, we need to introduce a person with an age equal to the previous average age plus the total number of individuals plus 1.
Obviously, the larger n, that is, the greater number of the individuals who make up the group, the harder it will be to find someone old enough to increase that average.
And similarly, if we want to reduce the average by one half, (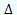 = -1), we get that:
= -1), we get that:
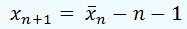
Which means that if n is large enough, it will be impossible to bring down the mean age in a year just by entering one person.
So the next time we visit a competition ballroom dancing competition or game consoles, we will not feel strange among the public, since the average age will barely suffer by our presence ...
If you arrived here, and want to tell us any comment on this topic, please send us an e-mail with the following link: contact@matifutbol.com . We greatly appreciate your help, as your comments are helpful to improve our site.
If you liked our riddle, you can share it in facebook or in twitter .
And if you want to be informed about our new publications, you can follow us in our facebook and twitter profiles.
Return to the first half
Go to the Championship to see more logic teasers.