The prodigious memory of Van Bommel
FIRST HALF
PSV Eindhoven is going home from the match they played yesterday evening vs. Feyenoord.
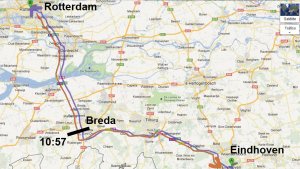
After sleeping in Rotterdam, the bus has left Rotterdam at 10:00 a.m. road to Eindhoven.
At one point, Mark Van Bommel, who boasts about his extraordinary memory, says: 'Yesterday we went through this place just at this very hour'.
His teammates do not quite believe him, but in his insistence, they decide to see if he's right. To confirm this, they remember that some PSV supporters where beside the road to wave to them at a place near the town of Breda, so they decide to call the president of the PSV Supporters' Club of Breda, in order to see if he knew at what time the bus had gone through Breda on Saturday and Sunday.
And indeed, the Club's president confirms that on both Saturday and Sunday they waved to the players in Breda at 10:57 hours.
Van Bommel's teammates insist he's been very lucky, and propose him a bet, on whether he will be able to do the same in all journeys of the Dutch league (Eredivisie).
Knowing that Van Bommel han an excellent memory, able to recall places and related times without problem, and that PSV bus always begins its outward journeys at 10:00 a.m., they sleep in the match town, and also start the return journey at 10:00 a.m. on the next morning, do you think that Van Bommel should accept the bet?
In other words, do you think that in every journey there will be a place for which the bus goes through at the same time on both the outward and the return journeys?
Go to the second half to discover the solution
SECOND HALF
A priori, it doesn't seem logical that the bus necessarily have to go through the same point at the same time on the outward and the return journeys, even though both departs are at the same hour.
In fact, there are numerous factors that influence every journey: the bus can go faster, or slower, or stop to filling up with fuel. Sometimes it will stop for a break, or because of a tyre puncture, sometimes it will find a traffic-jam by an accident ...
Therefore, it seems quite improbable that there should be a point in the road where the bus goes through both days at exactly the same time.
And nevertheless, it will happen every journey, as you'll see. If we are to address this problem in a direct way, we'll find many difficulties. Therefore, in this case we should study the problem from another angle, from which the problem seems really simple.
We can think of two buses leaving at the same time, one from Eindhoven and the other one from Rotterdam. This view does not affect the conditions of the problem, nor at what time the bus will pass through each point of the route. Thus, we can see clearly that there will be a moment when the two buses necessarily will meet somewhere in the road, that is, the two buses will be at the same time in the same place.
And this will happen every time. Sometimes the place will be closer to home, and sometimes closer to the destination, sometimes it will be sooner, and others will be later. But there will be always a cross in their way.
That's what happens with PSV bus, which is only one bus, but traveling on different days. On every journey back there will be a place at which the bus was going through the previous day at the same time.
So Mark Van Bommel should to take advantage of his extraordinary memory and accept his teammates bet.
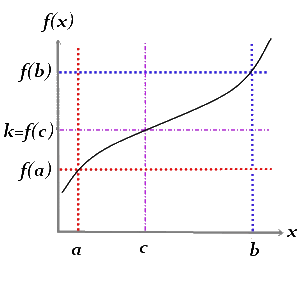
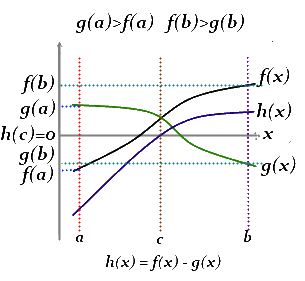
A more academic analysis of this problem leads us to solve it by using the Intermediate value theorem. This theorem states that if a function f is continuous on a closed nonempty interval [a, b] belonging to the set R of real numbers, and k is a real number between the values f(a) and f(b), there exists at least one interior point c on the interval [a, b] where f(c)=k. In like manner, if f and g are continuous functions on the interval [a, b] and we verify that g(a)>f(a) and f(b)>g(b), then there must exist a number c on the interval (a, b) such that f(c) = g(c).
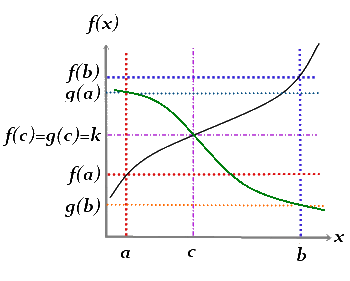
We can solve it in an even more elegant way with Bolzano's theorem , which is a particular case of the Intermediate value theorem. This theorem states that if f is a continuous function on the interval [a, b] and f(a)·f(b) < 0, that is, f(a) and f(b) differ in sign, then there exists a real number c on the interval (a,b) such that f(c) = 0. And if we have two continuous function f(x) and g(x) defined on a nonempty interval [a, b] of R, such that g(a)>f(a) and f(b)>g(b), and we define h(x) = f(x) - g(x), there is always a real number c on the interval (a, b) such that h(c) = 0.
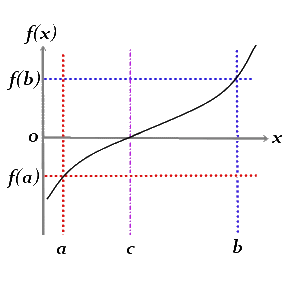
In our particular case, we define f(x) as the function that indicates the km. number of the road in which the bus is at time x in the outward journey, setting Eindhoven as km. 0 and Rotterdam as km. 110. So, if the bus arrives at Rotterdam at time x1, we define f(x) on the interval [0,x1], with f(0) = 0 and f(x1) = 110.
We also define g(x) as the function that indicates the km. number of the road in which the bus is at time x in the returning journey, also setting Rotterdam as km. 110 and Eindhoven as km. 0. So if the bus arrives at Eindhoven at moment x2, we define g(x) on the interval [0,x2], with g(0) = 110 and g(x2) = 0.
And finally we define function h(x) = f(x) - g(x) on the interval [0, min(x1,x2)]. We can see that the function fulfills the condition of Bolzano's theorem, so necessarily there will be a moment c so that h(c) = 0, or what is the same, f(c) = g(c).
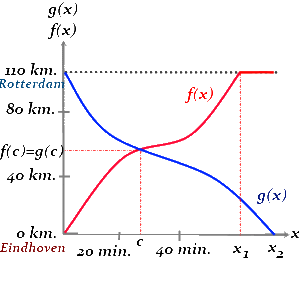
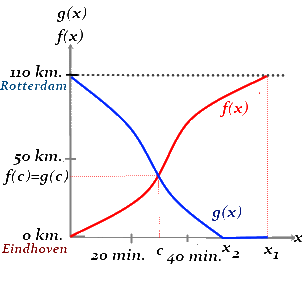
That way we demonstrate that in outward and return journeys, there's always a kilometer point f(c) where the bus goes through at the same time c. Therefore, Van Bommel will always have the opportunity of winning the bet, and knowing his extraordinary memory, he certainly will.
If you arrived here, and want to tell us any comment on this topic, please send us an e-mail with the following link: contact@matifutbol.com . We greatly appreciate your help, as your comments are helpful to improve our site.
If you liked our riddle, you can share it in facebook or in twitter .
And if you want to be informed about our new publications, you can follow us in our facebook and twitter profiles.
Return to the first half
Go to the Championship to see more logic teasers.
