The troubled stadium gates
FIRST HALF
Final match of Euro 2012 in Kiev / Kyiv. The national teams from Spain and Italy compete for the championship trophy.
 |
vs. | 
|
The referee whistles the final of the match, the winner celebrates the victory, and people start to leave the stadium. Because of an electronic problem, the exit doors are blocked, so that we have only 2 open emergency gates for the public to go out.
After the initial confusion, people begin to realize the problem and start to leave the stadium. Some people left the stadium in the first minute, and every minute there's outside the stadium twice as many people as in the previous minute.
Finally, after 10 minutes, the stadium is completely empty.
Imagine that, instead of 2 doors, security guards has managed to open 4 gates, and people have been leaving the stadium in the same manner as described,
How many minutes would have been necessary to empty the stadium in this case?
Go to the second half to discover the solution
SECOND HALF
First, it seems that if people have evacuated the stadium in 10 minutes through 2 gates, with 4 open doors the stadium should be empty in 5 minutes (half the time). But, obviously, that's a wrong calculation.
Let`s go to minute 10. Now all the public is out of the stadium. If we said that every minute that passes, people outside the stadium doubles, this means that at the end of minute 9, outside the stadium there was half the people than at the end of minute 10. Ie half the total spectators of the match.
In other words, at the end of minute 9, half the public was outside the stadium, and the other half was still inside. Therefore, if in 9 minutes half the public has come out through the 2 open doors, the other half of the public could have come out through another 2 open doors in these 9 minutes . Which means that it takes 9 minutes, and not 5 minutes, as it might seem initially, to leave the stadium if we open 4 gates.
Let's see another way:
Suppose that in the first minute 50 people go out per gate, that is, a total of (50 by 2 doors=) 100 people. After the second minute , we double the people outside the stadium (200). We continue with the same progression, we'll have 400 people in 3 minutes, 800 people after 4 minutes... and so on until to the minute 10. Let's see how this is reflected in the following table:
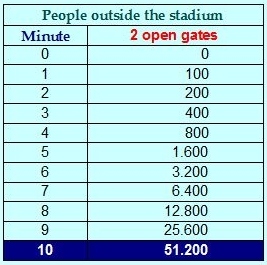
Now suppose that we open 4 gates, and in the first minute 50 people go out per gate (50 by 4 doors = 200 people), as in the previous case. Let's see what happens:
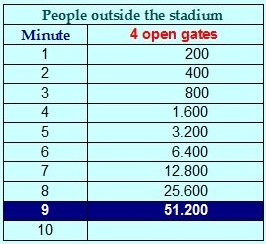
Until minute 9 we don't have all the people outside the stadium, and not in minute 5 as we initially supposed.
Can you imagine now what will happen if we open 8, 16, 32 or 64 gates? Curiously, every time we double the open gates, we only advance one minute!
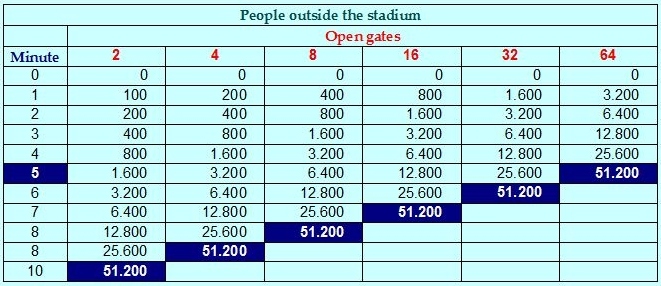
The key to this puzzle is that our brains display arithmetic progressions (linear functions) with no problems, but have many mental difficulties to imagine geometric sequences.
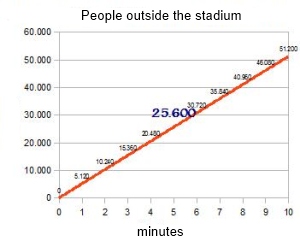
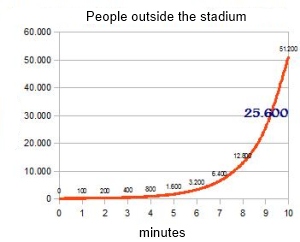
That's why we tend to assimilate geometric progressions to the arithmetic progressions, which leads us to errors such as we had in this example, or as that which led that ancient Indian king to offer a prize to the inventor of chess, in the form of grains of wheat/rice that grew from square to square in geometric progression. But that's another story...
If you arrived here, and want to tell us any comment on this topic, please send us an e-mail with the following link: contact@matifutbol.com . We greatly appreciate your help, as your comments are helpful to improve our site.
If you liked our riddle, you can share it in facebook or in twitter .
And if you want to be informed about our new publications, you can follow us in our facebook and twitter profiles.
Return to the first half
Go to the Championship to see more logic teasers.
