Vamos a regalar balones de fútbol
PRIMERA PARTE
Falta poco tiempo para que termine la Copa Mundial de Fútbol de Brasil 2014.
Los organizadores del Campeonato están pensando regalar unos balones oficiales del Mundial a los habitantes de Río de Janeiro.
Para ello, quieren llenar el estadio de Maracaná de balones de fútbol hasta la cubierta, y repartirlos el día antes de la ceremonia de clausura a todos los habitantes de la ciudad.
Regalarán todos los balones, excepto la última capa de balones que cubre el terreno de juego. Éstos los repartirán entre todos los asistentes a la ceremonia de clausura.
El problema es que no saben si habrá suficientes balones, primero, para repartir entre los habitantes de Río de Janeiro (población de 11.835.708 personas) y, segundo, para regalar a los asistentes al partido final (aforo de 82.238 espectadores).
¿Crees que cabrán los suficientes balones en el estadio?
Sigue a la SEGUNDA PARTE para conocer la solución.
SEGUNDA PARTE
Para resolver el problema, lo primero que tenemos que conocer son las dimensiones del estadio y las medidas de un balón de fútbol.
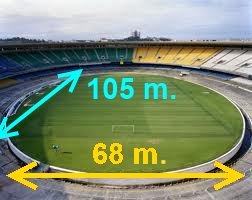El estadio de Maracaná presume de ser uno de los estadios más grandes del mundo. El terreno de juego, tras la reforma que se le ha efectuado, es un rectángulo de 105 metros de largo por 68 metros de ancho. Así que tenemos un área rectangular de 105 x 68 = 7.140 m2.
Ahora queremos conocer la superficie que ocupa un balón de fútbol. Las medidas oficiales aprobadas por la FIFA son: 21,65 - 22,29 cm. de diámetro. Vamos a utilizar para nuestros cálculos un valor intermedio de 22 cm. de diámetro (11 cm. de radio).
Para saber cuántos balones cabrán dentro del terreno de juego, no podemos dividir simplemente la superficie del campo de fútbol entre el área que cubre un balón, ya que los balones no ocupan toda la superficie, sino que que quedan huecos entre ellos.
Queremos, por tanto, optimizar el espacio ocupado por los balones, colocándolos de tal manera que quepan el mayor número posible de los mismos dentro del terreno de juego. Respecto a este tema, han sido numerosos los estudios que se han realizado, llegándose a la conclusión de que la mayor densidad de empaquetado posible (la mayor proporción de superficie ocupada por círculos de igual tamaño) es del 90,69%, que es cuando los balones adoptan una distribución de tipo hexagonal.
Así que calcularemos la superficie que cubre por un balón,
dividiremos la superficie total (7.140 m2) entre el área ocupada por un balón (0,038019 m2), y le aplicaremos el coeficiente de densidad (90,69%). Así obtenemos una cifra de 170.342 balones.
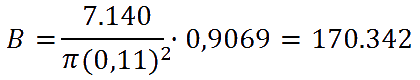
En este caso, no sólo contamos con los suficientes balones para regalar a los asistentes al partido, sino que podemos regalar 2 balones a cada uno de ellos.
Ahora vamos con el problema de si habrá suficientes balones para repartir entre todos los habitantes de Río de Janeiro, si llenamos el estadio.
Para resolver este problema necesitaremos 3 datos: el volumen de un balón, la capacidad del estadio, y el coeficiente máximo de densidad de empaquetamiento, esto es, el máximo porcentaje de ocupación del espacio que se puede conseguir optimizando la colocación de unas esferas de igual tamaño.
Vamos con el primer dato, el volumen de un balón. Anteriormente hemos establecido para nuestros cálculos que el diámetro del balón es de 22 cm. Así que, utilizando la fórmula para el volumen de una esfera, obtenemos que cada balón tiene un volumen de 0,005575 m3.
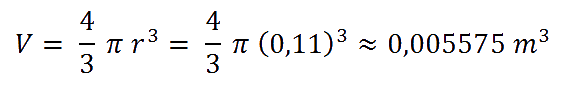
Ahora nos fijamos en las dimensiones del estadio de Maracaná. Sabemos que tanto la base del estadio como la cubierta tienen forma de elipse.
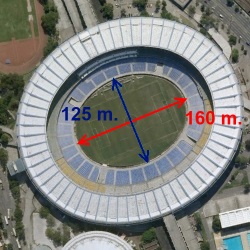
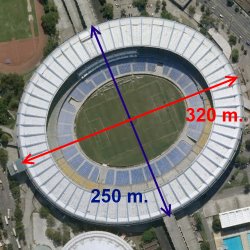
La elipse correspondiente a la superficie del campo de fútbol más el resto de terreno alrededor del mismo tiene una diagonal mayor de unos 160 metros y una diagonal menor de unos 125 metros. Por lo que la superficie total es de 15.707,96 m2.
Por otra parte tenemos que la altura máxima del estadio será de unos 32 metros.
Y sabemos que el estadio se va abriendo poco a poco conforme subimos de altura, de tal forma que la cubierta del estadio tiene también forma de elipse, con una diagonal mayor de unos 320 metros y una diagonal menor de aproximadamente 250 metros.
Con todos estos datos, obtenemos que el área de la cubierta es de 62.831,85 m2:
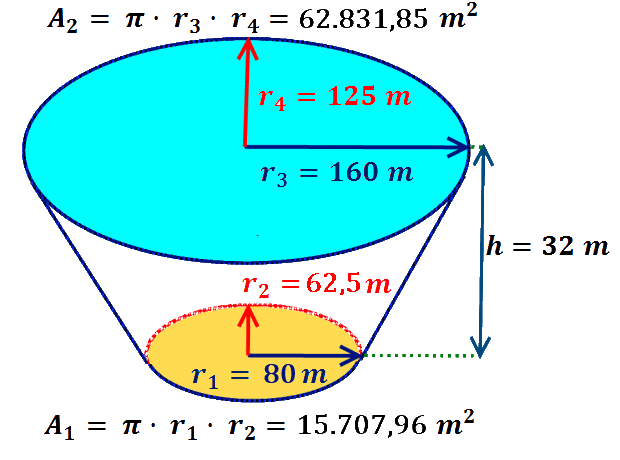
El cuerpo geométrico al que corresponde el volumen del estadio de Maracaná se denomina cono elíptico truncado invertido. Para calcular su volumen, bastarán unos minutos de búsqueda en internet hasta que encontremos la siguiente fórmula:
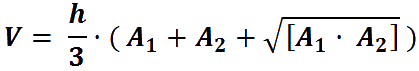
La aplicamos a nuestros datos, y obtenemos que el volumen a llenar con los balones será de 1.172.861 m3 (no tenemos en cuenta los espacios ocupados por porterías y demás objetos, ya que no tienen excesiva relevancia en dicho cálculo).
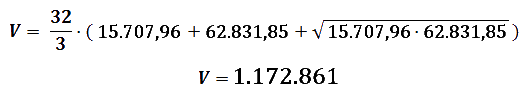
Y al igual que en el caso anterior, sabemos que para calcular cuántos balones cabrán, no podemos dividir simplemente el volumen del campo de fútbol entre el volumen de un balón, ya que los balones no ocupan el espacio por completo, sino que quedan huecos entre ellos.
Así, optimizando el espacio ocupado por los balones, colocándolos de tal manera que quepan el mayor número posible de los mismos, tenemos que la mayor densidad de empaquetamiento posible (el mayor porcentaje de espacio rellenado por unas esferas de igual tamaño) es del 74,084 %. O sea, que optimizando al máximo su colocación, los balones ocuparán un 74% del volumen del estadio.
En este caso, tendremos dos opciones para colocar los balones: el empaquetamiento compacto hexagonal, y el empaquetamiento compacto cúbico. Ambos métodos dan la misma densidad de empaquetamiento, y se corresponden con las dos disposiciones que puedes ver a la derecha.
Volviendo al tema que nos ocupa, ya podemos saber cuántos balones cabrán en Maracaná. Tenemos el volumen total del estadio, lo dividimos entre el volumen de un balón, y le aplicamos el coeficiente de densidad de empaquetamiento, con lo que obtenemos un total de 155.773.506 balones:
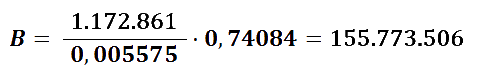
Y si a esta cifra le restamos los balones que vamos a regalar en la ceremonia de clausura, tenemos un total de 155.603.164 balones. Por tanto, los organizadores no sólo podrán regalar un balón a todos los cariocas (población de 11.835.708), sino que podrán dar un balón a gran parte de los brasileños (192.376.496 habitantes).
De esta forma, comprobamos que las dimensiones del estadio son suficientes para cumplir con los deseos de los organizadores del Campeonato. Otra cosa es si la organización del Mundial puede afrontar los gastos derivados de la compra de 155.773.506 balones, su transporte, su colocación en el estadio, su posterior distribución entre la población...
A título de anécdota, podemos decir que, por ejemplo, los gastos derivados sólo de la compra de balones (a 20 €/balón) sería de 3.058.030.589,24 €.
Y respecto a temas organizativos, tenemos que necesitaríamos 13.032 camiones de 90 m3 (los de mayor capacidad) para transportar todos los balones al estadio. Y que con 250 personas sacando dichos balones de los camiones, y otras 250 personas colocándolos dentro de él de una forma óptima (el perímetro exterior es de unos 800 m.), a razón de 5 segundos por balón, y trabajando durante las 24 horas, se tardarían más de 36 días en llenar el estadio de balones.
O que los citados camiones, de unos 18 m. de largo, puestos en hilera uno detrás de otro, formarían una caravana de 234 km. de largo. O que todos los balones pesarían un total de 66.982.607,78 kg (no sé si el césped del estadio quedaría apto para la actividad deportiva tras dicha operación). Y así podéis seguir realizando todos los cálculos que se os ocurran...
En esta historia tratamos del empaquetamiento compacto de círculos y esferas. Se trata de una de los temas matemáticos con más aplicaciones prácticas en la vida real, y de una trascendencia logística y económica importante.
La teoría del empaquetamiento compacto de objetos en espacios de n dimensiones fue ya tratada por Johannes Kepler, con su famosa 'conjetura de Kepler', en la que establecía que el empaquetamiento hexagonal era la forma más óptima de rellenar un espacio con esferas. Esta teoría fue asímismo complementada por los estudios de Carl Friedrich Gauss, para el caso de maximizar la ocupación de una superficie con círculos.
Por último, reseñar aquí el encuentro con un cuerpo geométrico no muy habitual, el cono elíptico, que nos permite tomar contacto con los estudios de Herón de Alejandría y su 'media heroniana', que nos permite calcular el volumen de dicho cuerpo.
Si llegaste hasta aquí, y deseas hacernos cualquier comentario sobre este tema, puedes enviarnos un correo con el siguiente enlace: contact@matifutbol.com. Agradecemos enormemente tu colaboración, ya que tus comentarios son de gran ayuda para mejorar nuestra página.
Si te gustó nuestro acertijo, puedes compartirlo en facebook o en twitter .
Y además quieres informarte de nuestras nuevas publicaciones, puedes seguirnos en nuestros perfiles en facebook, twitter, o por RSS
Vuelve a la primera parte
Regresa al Menú principal para ver más acertijos.
Matifutbol por Herminio López Arroyo se encuentra bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.
