Home page

Versión española Versió catalana

Search on Matifutbol:

Let's give away some balls.

FIRST HALF

Not much time for the Brazil 2014 FIFA World Cup ends.

Championship organizers are thinking about giving away official balls to all the Rio de Janeiro inhabitants.

To do this, they want to fill with balls the Maracana soccer stadium to the roof, and give away one ball for all Rio de Janeiro inhabitants, the day before the closing ceremony.

They'll give out all the balls, except the last layer of balls covering the pitch. These balls go to be distributed to all the closing ceremony spectators.

The problem is that they don't know whether there will be enough balls, in first place, to distribute among the Rio de Janeiro inhabitants (population of 11.835.708) and, in second place, to give to the final match spectators (capacity of 82,238 people).

Do you think that there will be enough balls in the stadium?

Go to the SECOND HALF to discover the solution

SECOND HALF

To solve the problem, the first things we need to know are the stadium size and the soccer ball size.

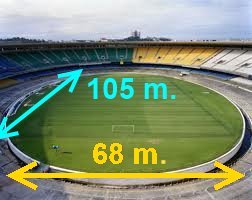Maracana Stadium boasts of being one of the largest stadiums in the world. The pitch, after the last reform, is a rectangle of 105 meters long by 68 meters wide. So we have a rectangular area of 105 x 68 = 7,140 m².

Now we want to know the area covered by a soccer ball. The official size adopted by FIFA are: 21.65 - 22.29 cm. in diameter. We will use for our calculations an intermediate value of 22 cm. in diameter (11 cm. radius).

To know how many balls will fit into the football field, we can't simply divide the football field surface by the area covered by a ball, because the balls don't cover the full surface, since there are some gaps between them.

We want to maximize the area covered by the balls, placing them in a way so that we fill as large proportion of the pitch surface as possible. There have been many researches about this issue, and their conclusion is that the highest possible packing density (the highest proportion of area covered by circles of equal size) is 90.69%, that is when the balls adopt an hexagonal layout.

So let's calculate the area covered by a ball,

divide the total area (7,140 m²) by the area covered by a ball (0.038019 m²), and apply the packing density ratio (90.69%). Thus, we get a sum of 170,342 balls.

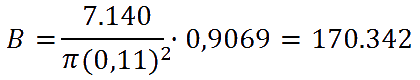
In this case, we not only have enough balls to give to the match spectators, but we can give away 2 balls to each one of them.

Now we go on to the question of whether there will be enough balls to give away to all the inhabitants of Rio de Janeiro, if we fill the stadium.

To resolve this problem we need 3 data: the volume of a ball, the capacity of the stadium, and the densest packing ratio, this is, the maximum fraction of space occupied by spheres that can be achieved by optimizing the arrangement of spheres of identical size.

Let's go with the first data, the volume of a ball. Previously we had established for our calculations that the diameter of the ball is 22 cm. So, using the formula for the volume of a sphere, we get that each ball has a volume of 0.005575 m³.

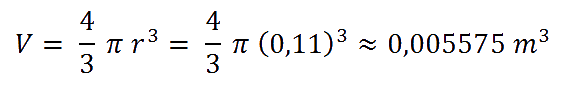
Now we go for the size of Maracana stadium. We know that both the lower base and the roof have the shape of an ellipse.

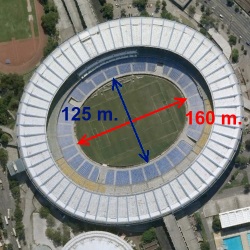
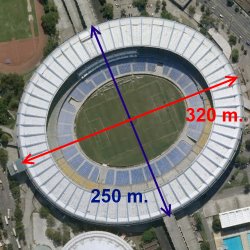
The ellipse corresponding to the area of the football pitch plus the rest of ground around it has a major diagonal of about 160 meters and a minor diagonal of about 125 meters. So the total area is of 15,707.96 m².

Moreover, we have that the maximum height of the stadium will be about 32 meters.

And we know that the stadium widens gradually as we ascend, and that the stadium cover is also elliptical, with a major diagonal of about 320 meters and a minor diagonal of about 250 meters.

With all these data, we get that the area of the cover is 62,831.85 m²:

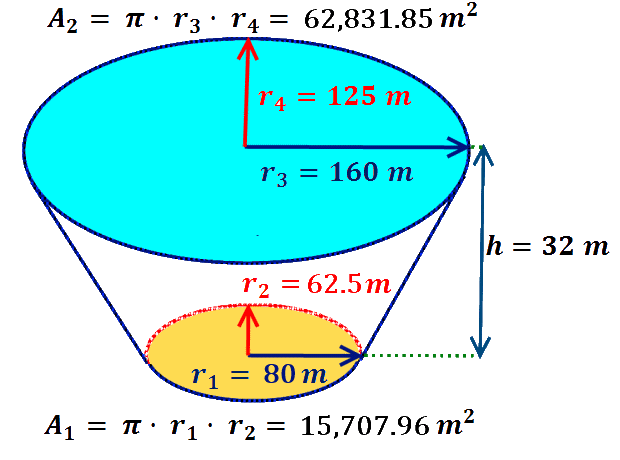
The geometric body corresponding to Maracana stadium is called an inverted truncated elliptical cone. To calculate its volume, we'll just need a few minutes in internet to find the following formula:

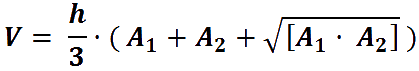
Let's apply it to our data, and we get that the volume to be filled with the balls will be 1,172,861 m³ (we can ignore the spaces occupied by goals and other objets, as they have a little relevance in this calculation).

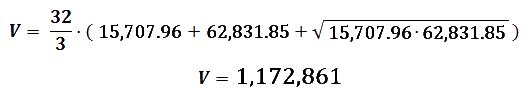
And like in the previous case, we know that for calculating how many balls will fit in the stadium, we can't simply divide the volume of the football field by the volume of a ball, since the balls don't occupy all the space, because of there are gaps between them.

Thus, optimizing the space occupied by the balls, placing them so to fill as large proportion of the space as possible, we get that the highest possible packing density (the highest percentage of space filled by spheres of equal size) is 74,084 %. In other words, making the most optimal arrangement, the balls will occupy a 74% of the volume of the stadium.

In this case, we have 2 options for placing the balls: the hexagonal close packing, and the cubic close packing. Both structures give the same packing density, and correspond to the 2 layouts you can see on the right.

We can now calculate how many balls will fit in Maracana. We have the total volume of the stadium, we divide it by the volume of a ball, and apply the packing density ratio, so we get a total of 155,773,506 balls:

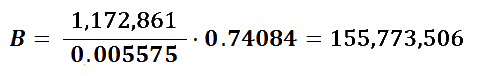
And if from this figure we subtract the balls they're going to give away at the closing ceremony, we've got a total of 155,603,164 balls. Therefore, the organizers can not only give out a ball to all the Rio de Janeiro population (11,835,708 inhabitants), but can also give a ball to most of Brazilians (192.376.496 inhabitants).

Thus, we see that the stadium size is big enough to comply with the wishes of the Championship organizers. Another subject is whether the organization can afford the costs of the purchasing 155,773,506 balls, their transport, their placement in the stadium, their distribution among the population...

As an anecdote, we can say, for example, that the cost for only buying the balls (20 €/ball) would be of 3,058,030,589.24 €.

And with regard to organizational issues, we would need 13,032 trucks of 90 m³ (the highest capacity) to carry all the balls to the stadium. And with 250 people taking these balls out of the trucks, and other 250 people placing them optimally within the stadium (the outer perimeter is about 800 m.), at a pace of 5 seconds per ball, and working 24 hours a day, it would take more than 36 days to fill the stadium with balls.

Or we can calculate that those trucks, of about 18 m. long, placed in a row one behind the other, will form a convoy of 234 km. long. Or that all the balls will weigh a total of 66,982,607.78 kg (I'm not sure if the stadium grass would be suitable for the game after this operation). And so on, you can continue to do all the calculations you can imagine...

In this story we treat about circle packing and sphere packing. This is one of the mathematical topics with most practical applications in real life, with an important logistical and economic significance.

The theory of packing of objects in n-dimensional spaces was already treated by Johannes Kepler, with his famous 'Kepler conjecture', which stated that the hexagonal close packing was the most optimal way to fill a space with spheres. Likewise this theory was supplemented by the studies of Carl Friedrich Gauss, in the case of maximizing the occupation of an area with circles.

Finally, note here that we meet with a not very usual geometric solid, the elliptical cone, which allows us to make contact with the studies of Hero of Alexandria and his 'Heronian mean', which allows us to calculate the volume of the geometric figure.

If you arrived here, and want to tell us any comment on this topic, please send us an e-mail with the following link: contact@matifutbol.com . We greatly appreciate your help, as your comments are helpful to improve our site.

If you liked our riddle, you can share it in facebook or in twitter .

And if you want to be informed about our new publications, you can follow us in our facebook and twitter profiles, or by RSS.

Return to the first half

Go to the Home page to see more logic teasers.