Mesut Özil y el punto de Fermat

PRIMERA PARTE
Se va a celebrar un partido amistoso entre el Real Madrid y el Internacional de Porto Alegre dentro de pocos días.
 |
vs. |  |
José Mourinho quiere reducir los espacios en el centro del campo, para defender de la mejor manera posible a los centrocampistas del Internacional de Porto Alegre.

Para ello, quiere disponer a su jugadores de la siguiente manera:
Xabi Alonso jugará en el centro del campo. Di María jugará por la banda derecha, 40 m. por delante de Xabi Alonso, y a 30 m. del centro del campo. También 40 m. por delante de Alonso, pero en la banda izquierda, y alejado igualmente 30 m. del centro del campo, se situará Cristiano Ronaldo.
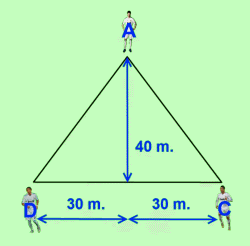
Y en una posición intermedia entre Xabi Alonso y la línea de Di María y Cristiano, y en el centro del campo, jugará Mesut Özil.
Mourinho quiere que la distancia entre Özil y los otros 3 jugadores sea mínima, para así poder realizar una mejor presión ante la salida del balón del Internacional de Porto Alegre y cubrir mejor los espacios.
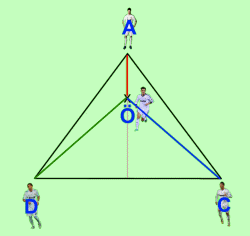
Para ello, la posición exacta de Özil será aquella en la que la suma de las distancias entre Özil y los otros 3 jugadores sea la mínima posible.
¿Eres capaz de averiguar en qué punto exacto se deberá colocar Özil?

Pasa a la segunda parte para conocer la solución

SEGUNDA PARTE
Algunos habrán pensado que Özil debe colocarse encima de la línea que une a Cristiano Ronaldo y Di María. Otras personas contestarán que deberá colocarse en el baricentro (intersección de las medianas o centro de gravedad) del triángulo isósceles formado por los otros 3 jugadores. Otros pensarán que deberá situarse en el circuncentro (centro de la circunferencia circunscrita, que pasa por los tres vértices del triángulo), en el incentro (centro de la circunferencia inscrita, tangente a los lados del triángulo), o incluso en el ortocentro (punto de intersección de las alturas).
Pero ninguna de estas soluciones es correcta. El resultado lo deberemos hallar de otra forma. Veamos cómo:
Tenemos a Alonso (A), Cristiano (C) y Di María (D) situados en el campo de la siguiente forma:
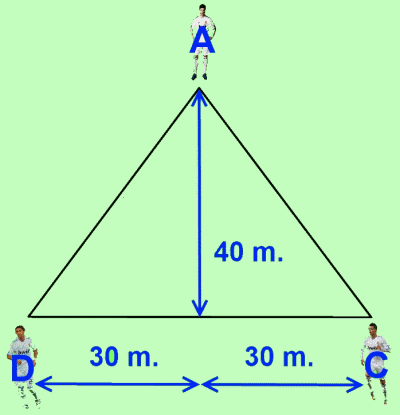
Situamos ahora a Özil (O) en un punto cualquiera de la altura del triángulo, ya que según las instrucciones de Mourinho, debe estar delante de Alonso y en el centro del campo:
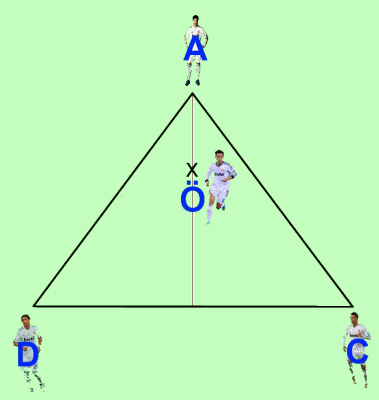
Nuestra misión es conseguir que la suma de las distancias a los otros 3 jugadores sea mínima, esto es, que la suma de los segmentos ÖA + ÖC + ÖD sea mínima.
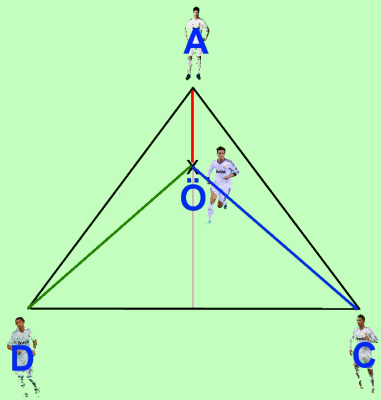
Para ello, vamos a girar el triángulo ACD 60º sobre Di María, en el sentido contrario a las agujas del reloj:
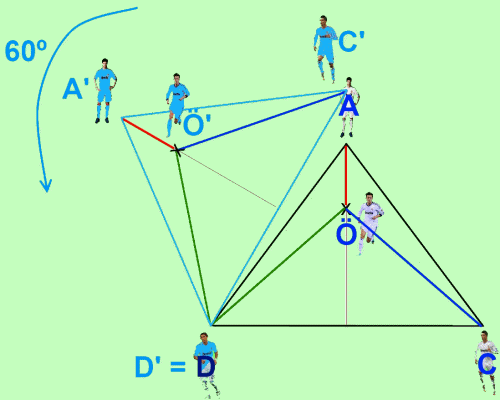
Nos fijamos ahora en estos dos triángulos: A'Ö'D' y ÖAD. Podemos comprobar que ÖA mide lo mismo que A'Ö', ya que los dos triángulos son idénticos, salvo que girados 60º
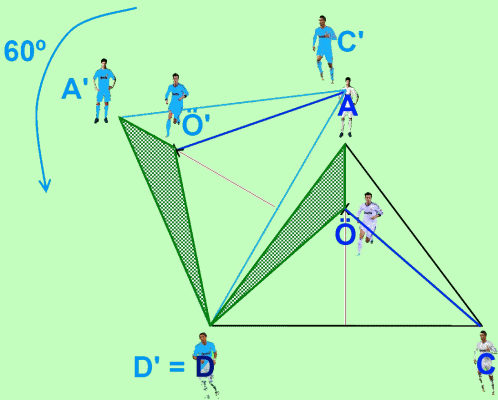
Ahora nos centraremos en el triángulo DÖ'Ö. Sabemos que el ángulo α es igual a 60º, y que DÖ y DÖ' miden igual. Por tanto, DÖ'Ö necesariamente tiene que ser un triángulo equilátero, de lo que se deriva que DÖ y Ö'Ö miden lo mismo.
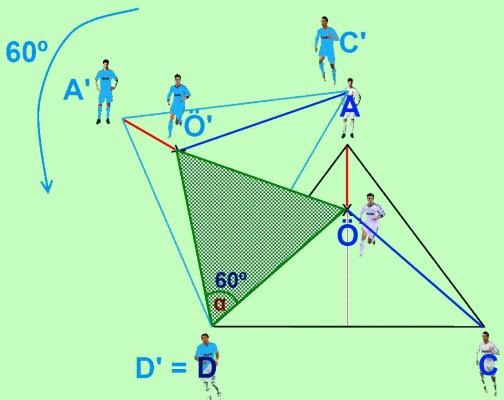
Con todo lo que hemos visto, tenemos ya resuelto el problema. Sabemos que ÖA = A'Ö' y que DÖ' = Ö'Ö. Por tanto, la suma de las distancias entre Özil y sus 3 compañeros es igual a: ÖA + ÖD + ÖC = A'Ö' + Ö'Ö + ÖC.
Vamos a ver a qué se corresponde esta suma en nuestro gráfico:
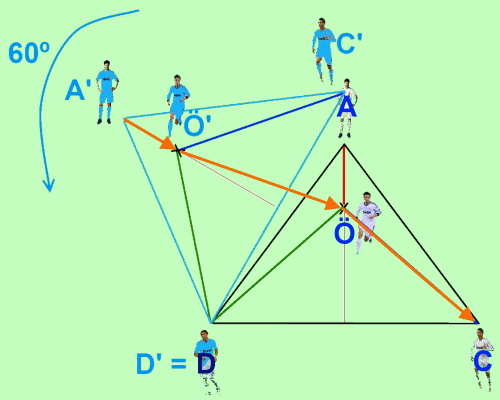
Efectivamente, se trata de la longitud del camino entre A' y C.
Y lo que queremos es que esta distancia sea la mínima posible. Para ello, aplicamos el conocido axioma de que 'el camino más corto entre dos puntos es la línea recta'.
Así que si lo que queremos es minimizar el camino entre A' y C, deberemos situar a Özil en la recta que une ambos puntos. De esta manera, cuando giremos el triángulo 60º, los caminos A'Ö' + Ö'Ö + ÖC y A'C se superpondrán.
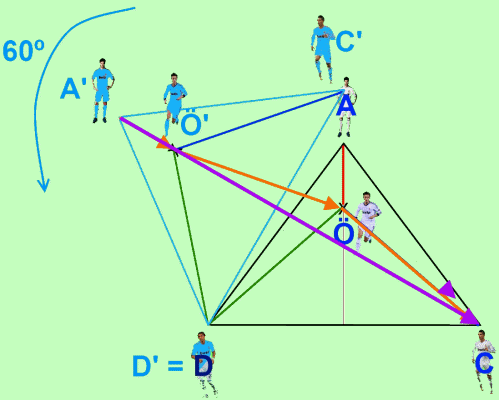
Y como sabemos que Özil debe estar en el centro del campo, esto es, sobre la altura del triángulo ADC, lo deberemos situar justo en el punto que en el que se cruza la altura con la recta A'C.
En el caso de que Özil pudiera situarse en cualquier punto dentro del triángulo formado por los otros 3 jugadores, pero no necesariamente en el centro del campo, deberíamos utilizar el mismo procedimiento que hemos realizado hasta ahora. De esta manera sabríamos que Özil debería situarse encima de la recta A'C, y para determinar el punto exacto en la misma, procederemos de forma análoga, esto es, giraremos la figura 60º, esta vez sobre Cristiano Ronaldo y en el sentido de las agujas del reloj. Y obtendremos así una nueva recta entre D y A'', que minimiza el camino entre los dos extremos. Y el punto en el que se cruzan ambas rectas sería donde debería colocarse Özil.
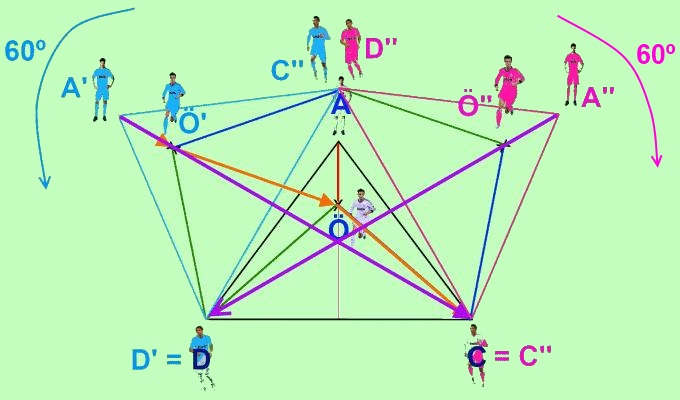
De esta forma habremos encontrado el punto exacto donde Mourinho quiere que Özil se sitúe dentro del terreno de juego, con el fin de contrarrestar el juego del los mediocampistas del Internacional de Porto Alegre.
Vamos a verlo ahora desde otro punto de vista más cuantitativo.
Tenemos el triángulo isósceles ADC, y su altura AB. Sabemos que Özil se va a situar en el centro del campo, por delante de Xabi Alonso, esto es, en un punto del segmento AB.
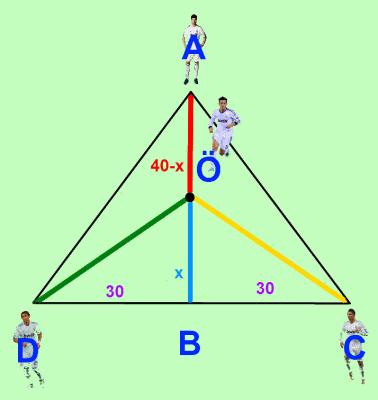
Si llamamos x a la distancia entre Özil y el punto B, Özil estará a una distancia 40-x de Xabi Alonso.
Nuestra misión es conseguir averiguar en qué punto tenemos que la distancia ÖA + ÖD + ÖC sea mínima.
Sabemos que ÖA es igual a (40-x), y que BD es igual a 30.
Según el teorema de Pitágoras, sabemos que:
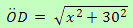
Y también conocemos que ÖC = ÖD
Con estos datos establecemos la función f(x) que nos calcula la suma de los 3 segmentos en función de dónde situemos a Özil
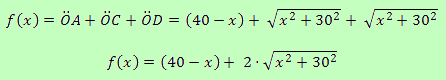
Queremos hallar x tal que f(x) sea mínima. Esto será así cuando la función derivada de x sea igual a 0, esto es, cuando f'(x) = 0.
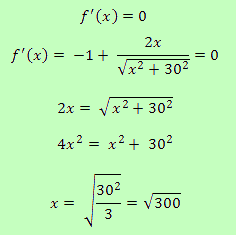
Así que tenemos que 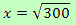
Podemos comprobar que este punto se corresponde con el punto desde el cual se ven los 3 lados bajo un ángulo de 120º.
E igualmente podemos comprobar también que la situación de este punto no depende de la distancia a la que se encuentre Xabi Alonso, siempre que el ángulo que forma con los otros dos jugadores no sea superior a 120º (en ese caso, Xabi Alonso y Özil compartirían el mismo lugar en el terreno de juego). El punto será el mismo si Xabi está a 40 m. de la línea CDque une a Cristiano y Di María que si está a sólo 20 m. Tan sólo depende de la separación entre estos 2 jugadores (CD = 2 BD), ya que:
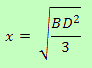
El punto donde se debe situar Özil se denomina punto de Fermat (también llamado punto de Torricelli). Constituye el primer punto notable del triángulo que se encontró después de la época de Euclides.
Debe su nombre al matemático francés del siglo XVII Pierre de Fermat que planteó el siguiente problema al científico italiano Evangelista Torricelli (1608 - 1647), descubridor de la presión atmosférica: 'Dado un triángulo acutángulo ABC construir un punto P tal que la suma de las distancias del punto a los 3 vértices A, B, C sea mínima'.
Hay quien dice que no fue Torricelli quien resolvió el problema, sino un discípulo suyo llamado Vicenzo Viviani, quien publicó la solución en su nombre, en 1659. Y otros atribuyen el planteamiento y la solución del mismo a Jakob Steiner (1796-1863). Además, ha habido numerosos matemáticos que se han encargado de estudiar este problema, como Hofmann, a través de su demostración gráfica de 1929, o Alfred Weber, quien en 1909 estudió el cálculo de localización óptima desde el punto de vista económico de modo que sea mínima la suma ponderada de las distancias desde un lugar a un conjunto de puntos dados, o Simpson (1710-1761), con su demostración geométrica, o Varignon y su máquina.
La primera solución que proponemos en este caso se corresponde con la publicada por Joseph Ehrenfried Hofmann en 1929, aunque también fue descubierta de forma independiente por Tibor Gallai entre otros.
La segunda solución sólo es válida para triángulos isósceles, y siempre que Özil se sitúe en la altura del triángulo.
En todo caso, este punto de Fermat aparentemente intrascendente cobra una importancia significativa en varios campos de las ciencias. Así, cuando queremos construir una carretera que conecte 3 o más ciudades, aplicaremos este teorema para encontrar el trazado ideal. O cuando una empresa con tres centros de producción quiere establecer una sede central en una localización óptima para minimizar los costes de transporte. O cuando queremos hallar el centroide o centro de un conjunto de masas. O para el diseño óptimo de circuitos eléctricos y redes de telecomunicaciones.
Y si aumentamos el número de puntos entre los que queremos optimizar su conexión, nos encontramos con el problema del árbol de Steiner, que es un problema de optimización combinatoria consistente en buscar la interconexión más corta para un conjunto de elementos dado. El punto de Fermat da una solución al problema general de la mediana geométrica, cuando el número de puntos en el plano es igual a 2, y al problema del árbol de Steiner para 3 puntos.
Si llegaste hasta aquí, y deseas hacernos cualquier comentario sobre este tema, puedes enviarnos un correo con el siguiente enlace: contact@matifutbol.com. Agradecemos enormemente tu colaboración, ya que tus comentarios son de gran ayuda para mejorar nuestra página.
Si te gustó nuestro acertijo, puedes compartirlo en facebook o en twitter .
Y además quieres informarte de nuestras nuevas publicaciones, puedes seguirnos en nuestros perfiles en facebook, twitter, o por RSS
Vuelve a la primera parte
Regresa a la Clasificación si quieres ver más acertijos.


Matifutbol por Herminio López Arroyo se encuentra bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.