Mesut Özil and the Fermat point.

FIRST HALF
The league match between Real Madrid and F.C. Barcelona will take place in a few days.
 |
vs. |  |
José Mourinho wants to plug the gaps in midfield, and let less space for Barcelona midfielders.

To achieve this, he wants to position his players as follows:
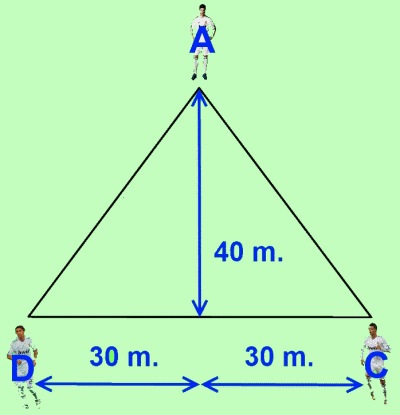
Xabi Alonso will play in the centre of the pitch. Di Maria will play down the right, 40 m. ahead of Xabi Alonso, and 30 m. from the centre of the field. Also 40 m. ahead of Alonso, but on the left wing, and also 30 m. away from the centre of the field, we'll find Cristiano Ronaldo.
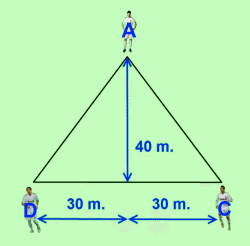
And Mesut Özil will play in an intermediate position between Xabi Alonso and the line Di María - Cristiano, and also in the centre of the pitch.
Mourinho wants to minimize the distance between Özil and the other 3 players, so they can do a better pressure on the ball out of Barcelona and better cover the gaps.
Thus, the exact position of Özil will be that in which the sum of the distances between Özil and the other 3 players is the minimum possible.
Can you figure out in which exact point Özil should be placed?

Go to the second half to discover the solution

SECOND HALF
Some people would have thought that Özil should be placed on the line Cristiano Ronaldo - Di María. Others would reply that he should be placed on the centroid (intersection of the medians or center of gravity) of the isosceles triangle formed by the other 3 players. Others will think that he should be at the circumcenter (center of the circumcircle, which passes through the three vertices of the triangle), on the incenter (center of incircle, tangent to the sides of the triangle), or even on the orthocenter (intersection point of altitudes).
But any of these solutions is correct. The result must be found another way. Let's see how:
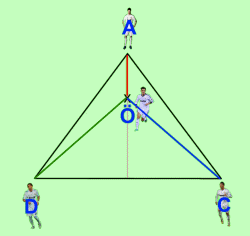
We have Alonso (A), Cristiano (C) and Di María (D) situated in the pitch as follows:
We put now Özil (O) at any point of the altitude of the triangle, since according to the instructions of Mourinho he should be ahead of Alonso and the center of the pitch:
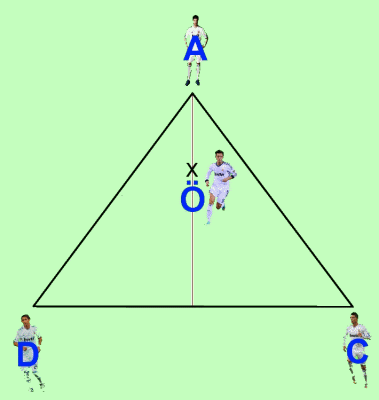
Our goal is to minimize the sum of the distances to the other 3 players, that is, achieving a minimal result for the sum of the segments ÖA + ÖC + ÖD.
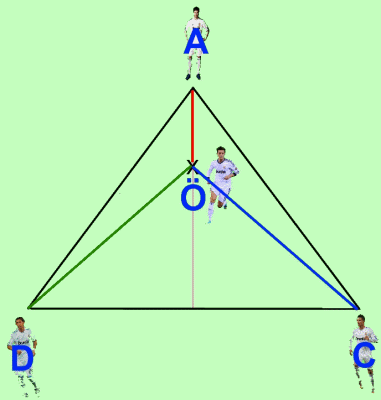
To do this, we turn the triangle ACD 60º counterclockwise on Di María:
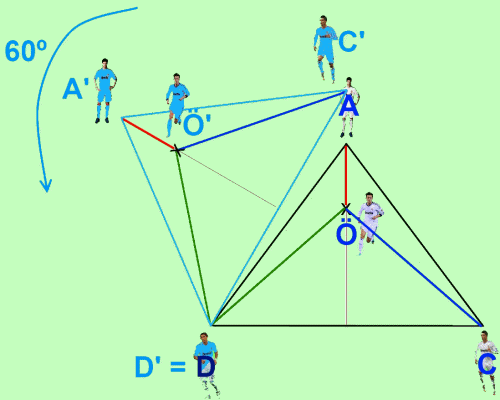
We now look at these 2 triangles: A'Ö'D' and ÖAD. We can verify that ÖA measures the same as A'Ö', since both triangles are identical, except by a 60º rotation.
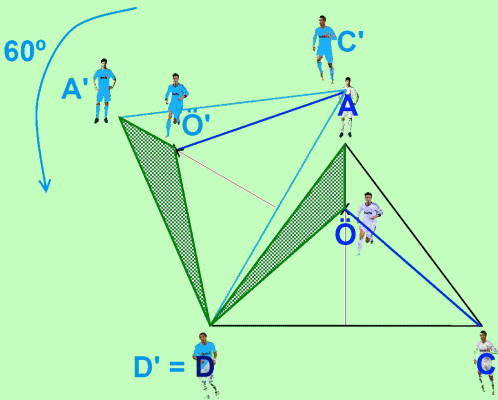
Now we will focus on the triangle DÖ'Ö. We know that the angle α equals 60º, and that DÖ and DÖ' have the same measure. Therefore, DÖ'Ö necessarily has to be an equilateral triangle, from which it's derived that DÖ and Ö'Ö have the same length.
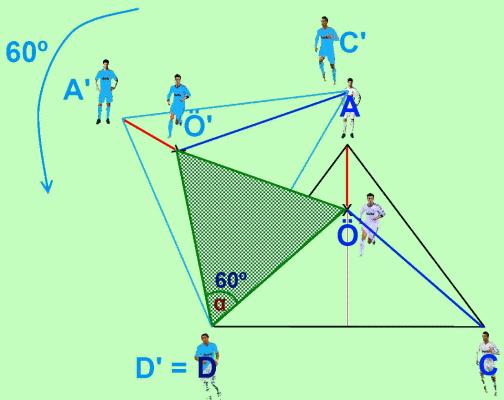
With all this data, we have already solved the problem. We know that OA = O'A' and that DO = OO'. Therefore, the sum of the distances (S) between Özil and his 3 playmates is equal to: ÖA + ÖD + ÖC = A'Ö' + Ö'Ö + ÖC.
Let's see what this sum corresponds to in our graph:
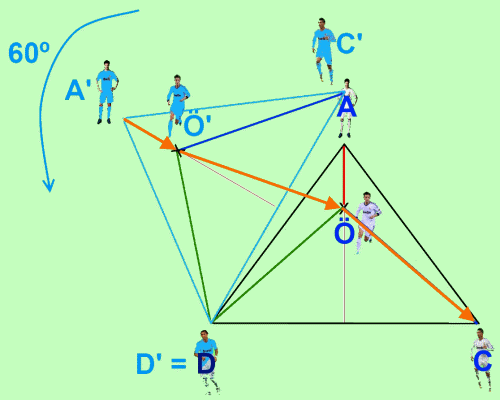
Indeed, this is the length of the way from A' to C.
And what we want is to reduce this distance to the minimum possible. To do this, we use the well-known axiom which states that 'the shortest distance between 2 points is a straight line'.
So if we want to minimize the distance between A' and C, we must position Özil in the line connecting the 2 points. Thus, when we turn the triangle 60º, the paths šA'Ö' + Ö'Ö + ÖC and A'C overlap.
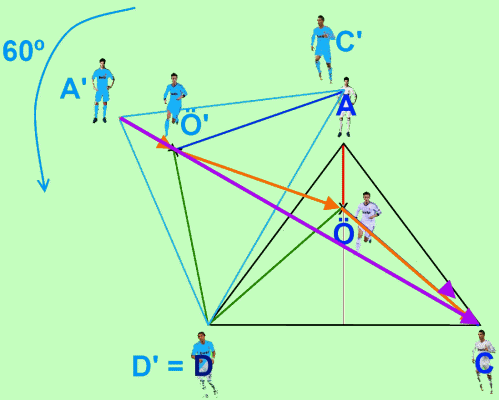
And as we know that Mourinho wants to put Özil at the center of the field, on the altitude of the triangle ADC, we have to position him on the point where this altitude intersects the line A'C.
In case that Özil could move to any point within the triangle formed by the other 3 players, but not necessarily in the center of the field, we should apply the same procedure. This way, we know that Özil should be placed on the line A'C, and to determine the exact point in it, we would proceed analogously: we turn the figure 60º, this time on Cristiano Ronaldo and clockwise. And so we get a new line between D and A'', which minimizes the path between the 2 extremes. And the point where the 2 lines intersect is where we have to place Özil.
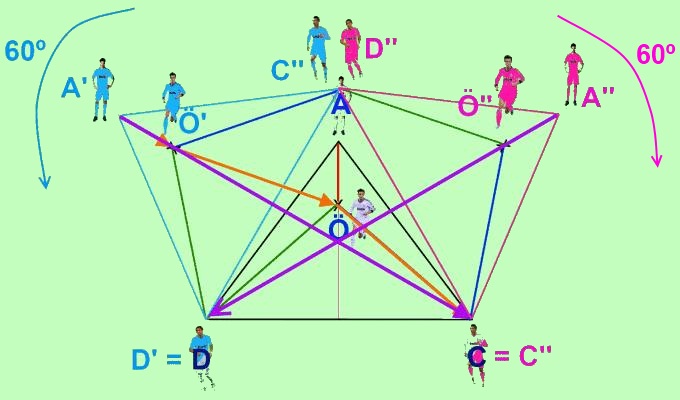
Thus we have found the exact point where Mourinho wants to place Özil in the pitch, in order to counter the game of FC Barcelona midfielders.
Let's see it now from another quantitative point of view.
We've got an isosceles triangle ADC, and its altitude AB. We know that Özil is to be located in the center of the pitch, ahead of Xabi Alonso, that is, in a point of the segment AB.
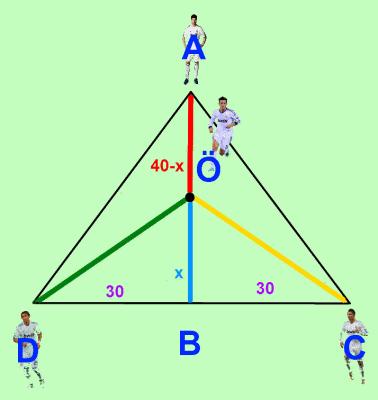
If we call x the distance from Özil to point B, Özil is at a distance of 40-x from Xabi Alonso.
Our mission is to find our at which point the distance ÖA + ÖD + ÖC is minimal.
We know that ÖA is equal to (40-x), and that BD equals 30.
By applying Pythagorean theorem, we have:
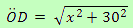
And we also know that ÖC = ÖD
With these data we set a function f(x) which calculates the sum of the 3 segments based on where we put Özil
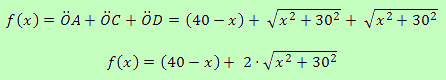
We want to find x such that f(x) is minimal. This will happen when the derivative function of x is equal to 0, that is, when f'(x) = 0.
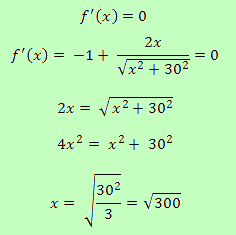
So we get 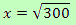
We could check that this point corresponds to the point from which you can see the 3 sides of the triangle from a 120º angle.
And likewise we can also check that the situation of this point doesn't depend on the distance from Xabi Alonso, whenever the angle that Xabi draws with the other 2 players is smaller than 120º (in such case, Özil should stand at the same place in the pitch than Xabi Alonso, in the vertex). The point will be the same if Xabi is 40 m. far from the line between Cristiano and Di María that if he's only 20 m. far from it. It only depends on the separation between these 2 players (CD = 2 BD), because:
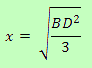
The point where Özil should be placed is called the Fermat point (also called Torricelli point). It`s the first notable point of the triangle that was found after the time of Euclid.
Named in honor of the 17th century French mathematician Pierre Fermat who posed the following problem to the Italian scientist Evangelista Torricelli (1608 - 1647): 'Given an acute-angled triangle ABC, construct a point P such that the sum of the distances from it to the 3 vertices A, B and C is the minimum possible'.
Some people say that it was not Torricelli who solved the problem, but a disciple called Vicenzo Viviani, who published the solution in his name, in 1659. And others attribute the approach and its solution to Jakob Steiner (1796-1863). In addition, there have been many mathematicians who have been studying this problem, as Hofmann, with his graphic demonstration in 1929, or Alfred Weber, who in 1909 studied the calculus of the optimal location from an economic point of view so to minimize the weighted sum of the distances from a place to a set of given points, or Simpson (1710-1761), with his geometric proof, or Varignon and his machine.
The first solution we propose in this case corresponds to that published by Joseph Ehrenfried Hofmann in 1929, which was also discovered independently by Tibor Gallai among others.
The second solution is only valid for isosceles triangles, and assuming that Özil is in the altitude of the triangle.
In any case, this seemingly inconsequential Fermat point assumes an especial importance in various fields of science and technics. So, when we want to build a road connecting 3 or more cities, we will apply this theorem to find the ideal line. Or when a company with 3 production centers wants to establish a headquarters in an optimal location to minimize transport costs. Or if we want to find the centroid or center of mass of a set of masses. Or for the optimal design of electrical circuits and telecomunication networks...
And if we increase the number of points between which we want to optimize their connection, we find the Steiner tree problem, which is a combinatorial optimization problem for seeking the shortest interconnection for a given set of elements. The Fermat point also gives a solution to the general problem of the geometric median, when the number of points in the plane is equal to 2, and to the Steiner tree problem for 3 points.
If you arrived here, and want to tell us any comment on this topic, please send us an e-mail with the following link: contact@matifutbol.com . We greatly appreciate your help, as your comments are helpful to improve our site.
If you liked our riddle, you can share it in facebook or in twitter .
And if you want to be informed about our new publications, you can follow us in our facebook and twitter profiles, or by RSS.
Return to the first half
Go to the Championship to see more logic teasers.