Menú principal

Versión española Versión americana English version

Segueix-nos

Busca en Matifutbol:

La decisió de Llorente

PRIMERA PART

Fernando Llorente s'enfronta a una difícil decisió. Vol jugar l'any que ve a la Premier League anglesa, i hi han 2 clubs interessats en la seva contractació: el Tottenham Hotspur F.C. i l'Aston Villa F.C. A Fernando li agraden tots dos equips per igual.

Ambdòs clubs volen una resposta ràpida, ja que necessiten incorporar un davanter als seus equips de forma urgent. Les condicions dels dos contractes seran exactament iguals, llevat de l'import de la fitxa anual del jugador.

vs.

El problema és el següent. El Tottenham li farà l'oferta aquest divendres, i vol la contestació al mateix dia. No obstant això, l'Aston Villa li farà arribar la seva oferta el diumenge, sense saber quina decisió ha pres el jugador sobre l'oferta que li hagi realitzat el Tottenham.

Així que Llorente haurà de decidir el divendres per quin equip fitxarà, sense conèixer si l'oferta de l'Aston Villa serà millor o pitjor que la del Tottenham.

Aparentement, sigui quina sigui la decisió que prengui Llorente, té un 50% de probabilitat d'encertar en la seva decisió, i un 50% de equivocar-se'n.

Vegem quins són els casos possibles que es poden donar:

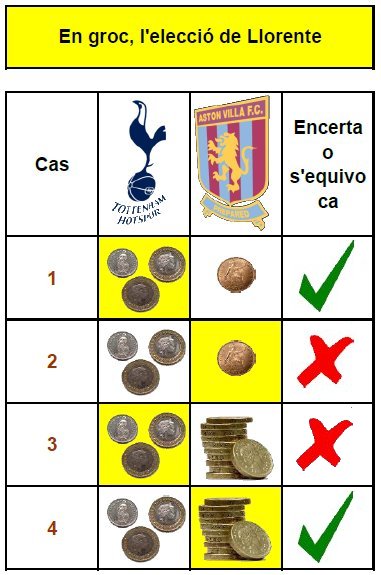
1. Accepta l'oferta del Tottenham, i l'oferta del Aston Villa és inferior.

2. Rebutja l'oferta del Tottenham, i l'oferta del Aston Villa és inferior.

3. Acsepta l'oferta del Tottenham, i l'oferta del Aston Villa és superior.

4. Rebutja l'oferta del Tottenham, i l'oferta del Aston Villa és superior.

Com podem comprovar, Fernando encerta amb la seva decisió en 2 dels 4 casos que es poden donar (1 i 4), i s'equivoca en els altres 2 (2 i 3).

Descartem el cas (5), que se produiria si les ofertes del Tottenham i de l'Aston Villa són iguals, ja que la posibilitat de que hi esdevingui és molt petita, i a més, sigui quina sigui la seva elecció, podem dir que Llorente sempre encerta, ja que li fa el mateix fitxar per un club que per l'altre.

Si no hi ha cap manera de saber per endavant l'oferta que realitzarà l'Aston Villa, creus que hi ha alguna forma d'incrementar la probabilitat de que Llorente encerti en la seva decisió?

Passa a la segona part per a conèixer la solució

SEGONA PART

Como ja hem vist, la probabilitat de que Llorente encerti en la seva elecció és del 50%. Aparentment, no sembla que pugui seguir cap estratègia pera incrementar aquest percentatge d'èxit. I no obstant això, sí que n'hi ha. Vegem de quina manera:

En aquest cas, la solució és d'allò més racional, i ve donada per allò que normalment ens aconsellarien el nostres pares o amics: el primer que haurà de fer Llorente és pensar quant vol cobrar les próximes temporades. I a partir d'aquí, podrá prendre la seva decisió d'una manera más encertada, també des del punt de vista matemàtic.

Així, si l'oferta que li fa el Tottenham el divendres és superior a les seves pretensions, l'acceptarà, i si és inferior, la rebutjarà y fitxarà per l'Aston Villa.

Anem a veure ara quins casos possibles es poden presentar:

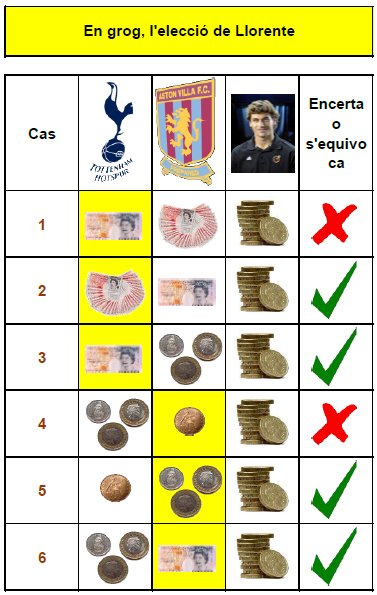
- Si el Tottenham li fa una oferta superior a les seves pretensions, i ell l'accepta:

1. El diumenge l'Aston Villa li ofereix més diners que el Tottenham.

2. L'Aston Villa li ofereix menys que el Tottenham, però més que les seves pretensions.

3. L'Aston Villa li ofereix menys que el Tottenham, i menys que les seves pretensions.

- Si el Tottenham li fa una oferta inferior a les seves expectatives, i ell la rebutja:

4. El diumenge l'Aston Villa li ofereix menys diners que el Tottenham.

5. L'Aston Villa li ofereix més que el Tottenham, però menys que les seves expectatives.

6. L'Aston Villa li ofereix més que el Tottenham, i més que les seves expectatives.

D'aquesta manera, podem comprovar que Llorente encertarà en 4 dels 6 casos (2, 3, 5 i 6), i s'equivocarà en només 2 d'ells (1 i 4).

(Aquí prescindim també del cas en què les ofertes siguin iguals, doncs ja van veure que era un cas molt improbable i que a més beneficiava a Llorente fos quin fos la seva elecció)

Amb aquesta estratègia, per tant, augmentem les probabilitats d'encert de 2/4 a 4/6.

Així que Llorente en tindrà prou amb reflexionar sobre quin import és el que vol cobrar, i actuar en conseqüència, per a aconseguir una probabilitat d'encert superior.

Ho veurem ara des del punt de vista matemàtic.

Tenim les 2 ofertes, una de superior import que l'altra, a las que anomenarem 'A' i 'a' ('A' la major, 'a' la menor). I tenim les pretensions econòmiques de Fernando Llorente, què anomenarem 'F'.

Els únics possibles casos que es poden donar, sabent que A>a, son els següents:

1) A > a > F

2) A > F > a

3) F > A > a

4) A = a

Como hem dit, Fernando Llorente acceptarà l'oferta del Tottenham si és superior a la xifra que desitja rebre.

En el primer cas (1), como les dues ofertes són superiors a las expectatives de Llorente, aquest escollirà la primera oferta, i fitxarà pel Tottenham, pel qual s'equivocarà un 50% de las vegades (unes vegades l'oferta major 'A' serà la del Tottenham, i d'altres vegades serà la del Aston Villa).

En el segon cas (2), quan una oferta sigui superior a les expectatives de Llorente, i l'altra sigui inferior, Fernando sempre encertarà, ja que si l'oferta del Tottenham és l'oferta 'A' l'acceptarà, i si és la 'a', la rebutjarà i acceptarà l'oferta 'A' de l'Aston Villa.

En el tercer cas (3), ambdues ofertes són inferiors a les expectatives de Llorente, de manera que aquest no escollirà la primera, i fitxarà per l'Aston Villa, equivocant-se el 50% dels cops (igual que al primer cas, unes vegades l'oferta major 'A' serà la del Tottenham, y àltres vegades serà la de l'Aston Villa).

En l'últim cas (4), ambdues ofertes són iguals, i com a Llorente el fa el mateix fitxar per un equip que per l'altre, podem dir que encerta sempre, sigui quina sigui la seva elecció).

Si anomenem:

P(C1) = probabilitat de que les dues ofertes superin les expectatives de Llorente, això és, que A>a>F (cas 1)

P(C2) = probabilitat de que les expectatives de Llorente es trobin entre ambdues ofertes, és a dir, que A>F>a (cas 2)

P(C3) = probabilitat de que ambdues ofertes siguin inferiors a les pretensions de Llorente, és a dir, F>A>a (cas 3)

P(C4) = probabilitat de que ambdues ofertes siguin iguals, independentment de que siguin superiors o inferiors a les pretensions de Llorente, és a dir, A=a (cas 4)

Com que necessàriament algun dels 4 casos s'ha de donar, tenim que:

P(C1)+P(C2)+P(C3)+P(C4)=1

Si ara anomenem P(x) a la probabilitat d'encert total, tindrem que serà igual a la suma de les probabilitats d'encert en cada un dels 4 casos possibles:

P(x)= P(x/C1)+P(x/C2)+P(x/C3)+P(x/C4)

Como ja hem vist, en els casos C1 i C3 la probabilitat d'encertar és del 50%, i en els casos C2 i C4 encertem sempre, el 100% de las vegades:

P(x)= 1/2 P(C1) + P(C2) + 1/2 P(C3) + P(C4)

P(x) = 1/2 (P(C1)+P(C2)+P(C3)+P(C4)) + 1/2 (P(C2)+P(C4))

P(x) = 1/2 + 1/2 P(C2) + 1/2 P(C4)

Atès que sempre existeix alguna probabilitat de que les pretensions de Llorente es trobin entre ambdues ofertes, és a dir, com P(C2) és sempre més gran que zero, i com la probabilitat de que les dues ofertes siguin iguals P(C4) també és més gran que zero, llavors la probabilitat global P(x) d'encertar sempre serà més gran que 1/2:

P(C2) > 0, P(C4) > 0 => P(x) = 1/2 + 1/2 P(C2) + 1/2 P(C4) > 1/2

Concloem, per tant, que amb aquesta estratègia Fernando Llorente millorarà les seves possibilitats d'obtenir un contracte més favorable.

Aquest problema consistent en triar el nombre més alt entre dos nombres ocults, que descobrim d'un en un, és una paradoxa en la què, per contrast amb d'altres, el resultat més favorable s'obté aplicant el sentit comú i resolent el problema de la forma en què habitualment ens enfrontem a aquest tipus de situacions (o al menys, de la forma en què hauriem d'enfrontar-nos-en a elles).

Quan augmentem el nombre d'opcions entre les que hem de triar, llavors hem d'utilitzar la teoria de la parada òptima, que consisteix en determinar quin és el moment més adient per prendre una decisió, de tal forma que maximitzem el profit, establint una regla òptima de parada. Aquest tipus de problemes els hi trobaréu en árees com l'estadística, les finances i la borsa, etc., així com a la nostra vida diària. Es tracta de decisions en les que hem d'acceptar una oferta en un moment determinat, sense possibilitat de marxa enrera (no podem reprendre ofertes passades) i no sabem quines ofertes tindrem en un futur.

La teoria de la parada òptima, desenvolupada entre d'altres per Franz Thomas Bruss, de la Universitat Lliure de Brusseles, qui va trobar la llei 1/e de la millor opció, pot èsser utilitzada a la pràctica per resoldre moltes situacions que se'ns presenten cada dia, com acceptar una oferta de treball o esperar les seguënts, comprar un determinat habitatge o seguir veient més, vendre unes accions en un moment determinat, o veure com hi evolucionen els dies següents...

Si has arribat fins aquí, i desitges fer-nos qualsevol comentari sobre aquest tema, pots enviar-nos un correu amb el següent enllaç: contact@matifutbol.com . Agraïm enormement la teva col·laboració, ja que els teus comentaris són molt útils per poder millorar la nostra pàgina.

Si t'ha agradat la nostra endevinança, pots compartir-la al facebook o al twitter .

I si a més vols informar-te'n de les nostres noves publicacions, pots seguir-nos als nostres perfils al facebook i al twitter

Regressa a la primera part

Torna a la Classificació si vols veure més trencaclosques.