Llorente's hard decision
FIRST HALF
Fernando Llorente faces a hard decision. He wants to play next year in the Premier League, and there're 2 clubs interested in signing with him: Tottenham Hotspur F.C. and Aston Villa F.C. Fernando likes both teams equally.
Both clubs want a quick answer, as they need to incorporate urgently a forward to their teams. The conditions of both contracts will be exactly the same, except for the amount of the annual fee of the player.
 |
vs. |  |
The problem states like this: Tottenham will make its offer on Friday, and they want Llorente's answer on the same day. Aston Villa will make its offer on Sunday, without knowing which decision the player has taken about Tottenham's offer.
That way Llorente will have to decide on Friday which team he's going to join, without knowing if Aston Villa's offer will be better or worse than Tottenham's.
Apparently, whatever decision Llorente takes, he has a 50% chance of succeeding in his decision, and a 50% of taking a wrong decision.
Let's see the possible scenarios that can occur:
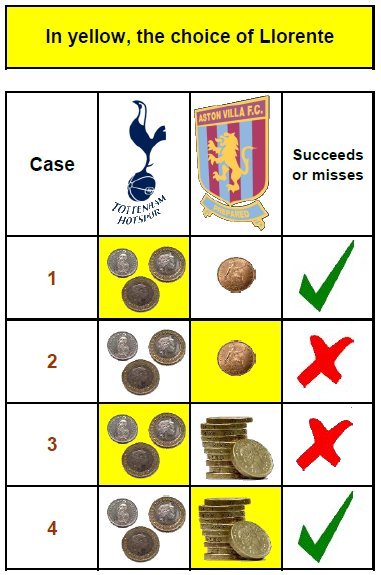
1. He accepts Tottenham's offer, and Aston Villa's offer is lower.
2. He rejects Tottenham's offer, and Aston Villa's offer is lower.
3. He accepts Tottenham's offer, and Aston Villa's offer is higher.
4. He rejects Tottenham's offer, and Aston Villa's offer is higher.
As we can see, Fernando succeeds with his decision in 2 of the 4 cases that can occur (1 and 4), and he's wrong in the other 2 (2 and 3).
We dismiss the (5) case, which would occur if the offers of Tottenham and Aston Villa are equal, since the possibility of ocurrence is very small, and besides, whatever his choice, we can say that Llorente is always right, because he doesn't want to sign specially for any of the clubs.
If there is no way to know in advance which offer Aston Villa will make, do you think there is any way to increase the probability that Llorente succeeds with his decision?
Go to the second half to discover the solution
SECOND HALF
As we have seen, the probability that Llorente succeeds in his choice is 50%. Apparently, it doesn't seem to exist any strategy to increase that success rate. And yes, there is one. Let's see how:
In this case, the solution is very rational, and is given by what our parents or friends would advise to us: the first thing Llorente should do is to think how much he wants to earn the next seasons. And from there, he can take his decision in a more accurate way, also from a mathematical standpoint.
So, if Friday's Tottenham offer exceeds his claims, he should accept it, and if it's lower, he should reject it and sign for Aston Villa.
Let's see now which possibles cases may occur:
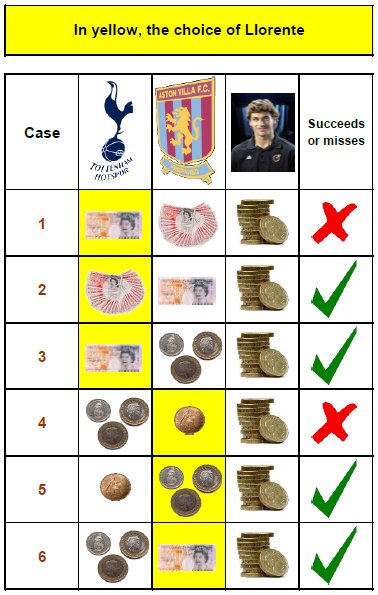
- If Tottenham offers more than to his claims, and he accepts:
1. On Sunday, Aston Villa offers more money than Tottenham.
2. Aston Villa offers less than Tottenham, but more than his claims.
3. Aston Villa offers less than Tottenham, and less than his claims.
- If Tottenham makes a lower offer than his claims, and he rejects it:
4. On Sunday Aston Villa offers him less money than Tottenham.
5. Aston Villa offers more than Tottenham, but less than his claims.
6. Aston Villa offers more than Tottenham, and more than his claims.
Thus, we can see that Llorente will succeed in 4 of the 6 cases (2, 3, 5 and 6), and will be wrong in only 2 of them (1 and 4).
(Here we also ignore the case in which the offers are equal, because as we saw before it was a very unlikely event and also benefited Llorente whatever his choice was).
With this strategy, therefore, we increase the probabilities of succeeding from 2/4 to 4/6.
So Llorente simply has to think on which amount he wants to earn, and act according to it in order to get a higher probability of success.
Let's have a look at it from a mathematical point of view.
We have 2 offers, one higher than the other, which we will call 'A' and 'a' ('A' the greatest, 'a' the smallest). And we have the economic claims of Fernando Llorente, that we'll call 'F'.
The only possible cases that may occur, knowing that A>a, are:
1) A > a > F
2) A > F > a
3) F > A > a
4) A = a
As mentioned, Fernando Llorente will accept Tottenham's offer if it exceeds the amount he wants to earn.
In the first case (1), as both offers are above Llorente's expectations, he will choose the first offer, and will join Tottenham team, so he will be wrong 50% of the time (sometimes the highest offer 'A' will be Tottenham's, and sometimes will be Aston Villa's).
In the second case (2), when an offer exceeds Llorente's expectations, and the other offer is lower, Fernando will always succeed, because if Tottenham's offer is 'A' he will accept it, and is it's 'a', he will reject it and accept offer 'A' from Aston Villa.
In the third case (3), both offers are below Llorente's expectations, so he will not pick the first one, and he will join Aston Villa, with a success of 50% of the time (as in first case, sometimes the highest offer 'A' will be Tottenham's, and sometimes will be Aston Villa's).
In the latter case (4), both offers are the same, and as Llorente doesn't like one team more than the other, we can say that he always succeeds, whatever his choice).
If we call:
P(C1) = probability that both offers exceed Llorente's expectations, that is, A>a>F (case 1)
P(C2) = probability that Llorente's expectations are among the 2 offers, that is, A>F>a (case 2)
P(C3) = probability that both offers are below Llorente's expectations, that is, F>A>a (case 3)
P(C4) = probability that both offers are equal, whter they are above or below the claims of Llorente, this is, A=a (case 4)
Necessarily one of the 4 cases must happen, so we have:
If now we call P(x) to the overall success probability, we have that it's eual to the success probability in each of the 4 possible cases:
As we have seen before, in cases C1 and C3 the success probability is 50%, and in cases C2 and C4 Llorente succeeds always, 100% of the time:
Since there is always a chance that Llorente's claims are among both offers, in other words, as P(C2) is always greater than zero, and as the probability that both offers P(C4) is also greater than zero, then the overall success probability P(x) is always greater than 1/2:
We conclude, therefore, that with this strategy Fernando Llorente will improve his chances of obtaining a more favorable contract.
This problem consists in choosing the highest number among two hidden numbers, that we discover one by one. This is a paradox in which, unlike other ones, we get the best result by applying our common sense and solving it by the way we often face this type of situations (or at least, by the way we should face them).
As we increase the number of available options, we must follow the optimal stopping theory, which consist in determine the optimal moment to take a decision, in order to maximize the profit, stablishing an optimal stopping rule. We find such kind of problems in different areas like statistics, finances and stock market, etc., as in our everyday life. It's about decisions we have to take on either accepting an offer at a precise moment, with no posibility of resuming a last offer, and without knowing which offer we'll have in the future.
The optimal stopping theory, performed among others by Franz Thomas Bruss, from the Free University of Brussels (Université Libre de Bruxelles), who found out the 1/e-law of best option, that we can use for solving lots of situations we face every day, like accepting a job offer or waiting for more, buying a house or looking for more, selling some stock options or waiting for a better moment...
If you arrived here, and want to tell us any comment on this topic, please send us an e-mail with the following link: contact@matifutbol.com . We greatly appreciate your help, as your comments are helpful to improve our site.
If you liked our riddle, you can share it in facebook or in twitter .
And if you want to be informed about our new publications, you can follow us in our facebook and twitter profiles.
Return to the first half
Go to the Championship to see more logic teasers.
