• Home page
• Links

English version Versión española Versión americana Versió catalana

Follow us

Search on Matifutbol:

Do you dare to count? A forward-and-back problem

FIRST HALF

England and Brazil are playing a friendly football match. Few minutes before the match starts, players from both teams are warming up on the pitch.

vs.

English players are running from sideline to sideline, according to the instructions their trainer has given them, and which are as follows:

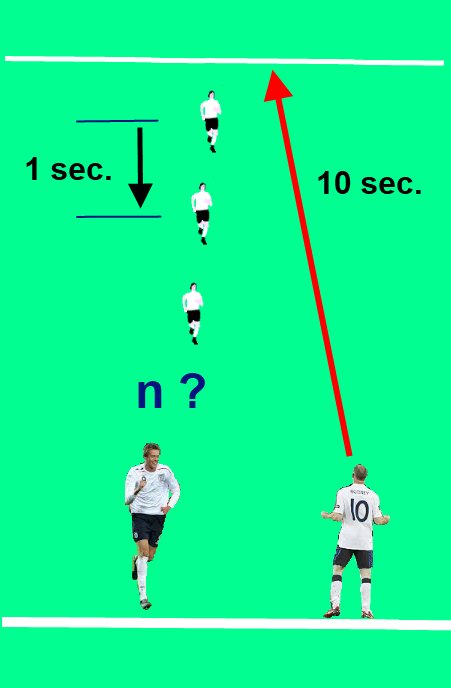
- Every second a player is given the starting signal from the sideline.

- They must complete the distance to the other sideline in 10 seconds, at a steady pace, following the foregoing player.

- Once a player gets to the other sideline, and without stopping, he will turn around and return to the original sideline at the same steady pace as in the forward way (10 seconds), and then he can go to the changing room.

Wayne Rooney is the last player to leave out. Just at the moment the trainer gives the starting signal, Peter Crouch reaches the sideline.

Can you estimate how many players Ronney will meet on his way to the other sideline?

Go to the second half to discover the solution

SECOND HALF

Some people answer that Rooney crosses 10 players: if he takes 10 seconds to get to the other side, and every second a player has left out the band, we do the cocient and we get this result: 10 players.

Other people think the same way, but they add, to the 10 players we have calculated, one more player, corresponding to Peter Crouch, who crosses at second 0:00. So they stand that Rooney will cross 11 players. And another group of people answer that he will meet with a larger or smaller number of players.

Let's see who's right.

The second option (11 players) is incorrect, because at the 10th second Rooney will not match anyone on the other side, that is, he will meet players at the seconds 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9, but not at second 10, since the previous player began his return way one second ago.

So, at first sight, the first reasoning seems correct. We have the time (10 seconds), the output frequency (1 player / second) and we obtain the result:

10 seconds * (1 player / 1 second) = 10 players

And this would be correct if Rooney still remains in the band. But here we must consider a third factor that we've fogotten: that Rooney is moving during these 10 seconds.

This means that Rooney will not meet a player every second of his route, but as both players are moving toward each other, they will complete the distance between them in half the time (0.5 seconds) to meet at half the distance. So, Rooney will cross with:

10 seconds * (1 player / 0.5 seconds) = 20 players

Look at it another way:

When Rooney leaves in the last place, there will be 10 of his team-mates traveling in the same direction to the opposite sideline, and other 10 teammates returning from there.

So when Rooney gets to the other side, he will necessarily have met them all, the 10 ones that are now returning, and the 10 that are now traveling in the same direction, who he will find them returning to the initial sideline as time goes by.

We can also solve the problem by a graphic, drawing the position of every player according to the initial sideline in every moment of his way. As you can see in the graphic below, the route of Rooney intersects the way of 20 team-mates (including Crouch, who meets on second 0:00).

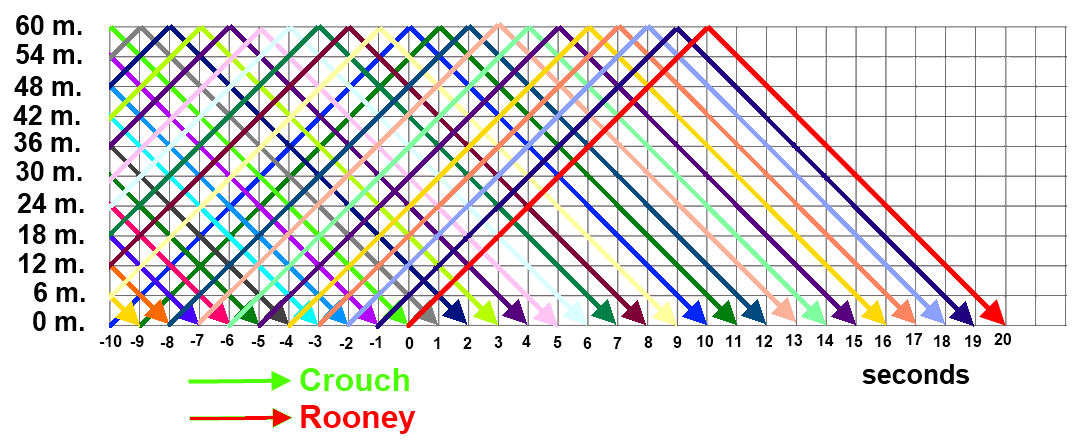
This is a new exercise in logical reasoning, in which our brain focuses on numeric variables (10 seconds, 1 player / second) and desestimates other apparently non-numeric fundamental variables: the speed and the direction of Rooney's movement.

This is a football version of the mathematical problem initially exposed by Charles-Ange Laisant on the ships that crossed in the path between Le Havre and New York, and later edited by the Brazilian recreational-mathematics writer Malba Tahan.

If you arrived here, and want to tell us any comment on this topic, please send us an e-mail with the following link: contact@matifutbol.com . We greatly appreciate your help, as your comments are helpful to improve our site.

If you liked our riddle, you can share it in facebook or in twitter .

And if you want to be informed about our new publications, you can follow us in our facebook and twitter profiles.

Return to the first half

Go to the Championship to see more logic teasers.