

El problema del reparto justo.

PRIMERA PARTE
 La Confederación Africana de Fútbol ha decidido disputar un partido en beneficio de Haití. El partido se celebrará en el estadio Soccer City de Johannesburgo. Para ello, han convocado a los mejores futbolistas del continente.
La Confederación Africana de Fútbol ha decidido disputar un partido en beneficio de Haití. El partido se celebrará en el estadio Soccer City de Johannesburgo. Para ello, han convocado a los mejores futbolistas del continente.
 por
por

Faltan pocas horas para que comience el partido. Samuel Eto'o y Didier Drogba han sido designados capitanes de los equipos rojo y azul, respectivamente.


Serán ellos quienes elijan a los jugadores de sus equipos. Y aquí es donde se plantea el problema.
Para efectuar el reparto de una forma más eficiente, se ordenan todos los jugadores por su calidad, de mayor a menor.

Comienza Eto'o eligiendo al primer jugador (E), luego elige Drogba (ED), luego Eto'o (EDE), luego Drogba (EDED), y así sucesivamente...
Cuando termina la distribución, Drogba se queja de que la calidad de su equipo es inferior a la del equipo de Eto'o, ya que en cada pareja de jugadores elegidos, el jugador elegido por Eto'o es mejor que el de Drogba: ED ED ED ED ED ED...

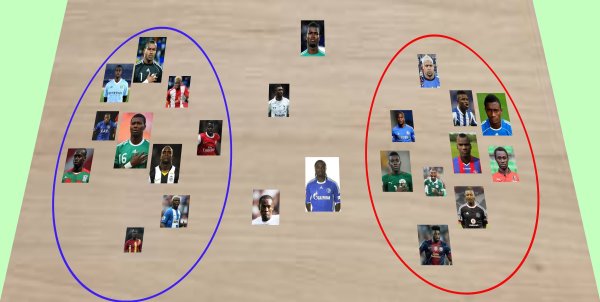
Por tanto, deciden hacer un nuevo reparto. Comienza esta vez eligiendo Drogba (D), luego elige Eto'o 2 jugadores (DEE), vuelve a elegir Drogba 2 jugadores (DEEDD), y así hasta el final.
Ahora es Eto'o quien se queja del reparto, ya que si bien la elección está más equilibrada (DEED DEED DEED...), resulta que de esta forma todos los porteros disponibles han quedado encuadrados en el equipo de Drogba, mientras que el equipo de Eto'o no cuenta con porteros...
Parece un problema irresoluble, sobre todo cuando a última hora se presenta un nuevo jugador, Boateng, de tal forma que ahora ¡hay un número impar de jugadores para repartir entre los 2 equipos!
¿Podrías ayudar a Eto'o y a Drogba para repartir los jugadores de tal forma que ambos queden satisfechos?
Pasa a la SEGUNDA PARTE para conocer la solución.

SEGUNDA PARTE
Dentro de las distintas posibilidades de reparto equitativo, también podrían haber pensado en esta otra: (DEED EDDE DEED EDDE DEED...) y en otras muchas combinaciones que aparentemente satisfacen la necesidad de igualdad entre los equipos.
Pero cualquier solución de este estilo es sólo viable siempre y cuando el salto de calidad entre todos los jugadores sea uniforme. Además, la llegada del último jugador desbarata por completo cualquier intento de reparto parecido a los descritos.
Con un número impar de jugadores, lo que podemos hacer asignar una 'valoración' a cada jugador en función de su calidad. Sumamos todos los puntos, y escogemos para cada equipo jugadores que sumen la mitad de dicha cifra.
Este método también tiene sus inconvenientes:
Primero, porque el total de puntos será divisible por 2 sólo en aproximadamente la mitad de las ocasiones (dependerá si otorgamos puntos de 0 a 10, de 1 a 5, de 1 a 100, etc).
En segundo lugar, porque la asignación de puntos a cada jugador se deberá realizar de una forma subjetiva, con la que no coincidirán necesariamente Eto'o y Drogba. Así, la igualdad de los dos equipos según la valoración de una tercera persona puede no ser percibida de igual forma por estos jugadores.
Tercero, porque es posible que no haya ninguna combinación de jugadores cuya suma de puntos sea exactamente igual a la mitad de los puntos totales obtenidos.
Y en cuarto lugar, porque aun siendo posible dividirlos en 2 equipos con igual puntuación, podrá ocurrir que, como en el ejemplo, todos los porteros queden encuadrados en un solo equipo, o que un equipo no tenga ningún delantero, o que todos los jugadores de un equipo sean zurdos...
Así que... ¿de qué forma podremos proceder para realizar un reparto que les resulte justo a ambos jugadores, Eto'o y Drogba?

En este caso aplicaremos una fórmula muy sencilla:
Encargaremos a cualquiera de los dos jugadores a que realice el reparto de los jugadores en dos equipos, de la forma más equitativa posible, y sabiendo que será el otro jugador quien escoja con qué grupo de jugadores se queda.
De esta forma, el jugador que reparte quedará satisfecho, pues sabe que ha realizado el reparto de la forma más equitativa posible, ya que será el contrario quien elija entre los dos equipos formados.
Y el jugador que elige también quedará satisfecho, pues entre los dos grupos habrá escogido el que piensa que tiene más calidad.
Así que de esta forma ya no habrá ningún impedimento para que se pueda por fin celebrar este interesante encuentro.
Este problema trata de un método muy válido para resolver problemas de repartos entre 2 personas que no son capaces de llegar a un acuerdo. Existe también una variante del mismo, en el caso de que sean 3 las personas entre las que debemos repartir un conjunto de elementos, un poco más difícil de poner en práctica, pero igualmente efectivo:
Imaginemos que Eto'o, Drogba y Boateng quieren disputar un torneo triangular. En este caso, dejaríamos que Eto'o, por ejemplo, realizase el reparto de los jugadores en tres equipos: rojo, azul y amarillo.
Ahora les damos a escoger a Drogba y a Boateng. Si cada uno de ellos escoge un equipo distinto, Eto'o se quedaría con el restante, y el tema estaría resuelto.
Si Drogba y Boateng quieren el mismo equipo, supongamos que el equipo rojo, entonces haremos lo siguiente: les daremos a escoger entre quedarse con el equipo amarillo o repartirse entre ellos los equipos rojo y azul. Si solo uno de ellos escoge el equipo amarillo, al otro le daremos el rojo (que era el que prefería inicialmente), y Eto'o se quedará con el azul.
Si los dos jugadores prefieren repartirse los equipos rojo y el azul, bastará que sigan el método descrito para el reparto entre dos personas, y Eto'o se quedará con el amarillo.
Y si ambos prefieren el equipo amarillo antes que repartirse el rojo y el azul, es porque los dos jugadores perciben que el equipo amarillo tiene más calidad que el azul (de otro modo hubiesen preferido repartirse entre ellos los conjuntos rojo y azul), por lo que en este caso deberemos ofrecerles a Drogba y Boateng que se repartan entre ellos los equipos rojo y amarillo de la forma descrita, y asignaremos el equipo azul a Eto'o.
Aquí mostramos un ejemplo más de lo que conocemos por pensamiento lateral. Se trata de una forma de abordar los problemas desde un punto de vista distinto al que normalmente utilizamos para enfrentarnos a ellos, enfocándolos de una forma indirecta y creativa.
Por último, queremos enviar desde esta página unas palabras de apoyo al pueblo de Haití, esperando que artículos como éste sirvan, además de para pasar un buen rato y para aprender algo de lógica matemática, para que no nos olvidemos tan pronto de los países que sufren catástrofes como la de ese país.
Si llegaste hasta aquí, y deseas hacernos cualquier comentario sobre este tema, puedes enviarnos un correo con el siguiente enlace: contact@matifutbol.com. Agradecemos enormemente tu colaboración, ya que tus comentarios son de gran ayuda para mejorar nuestra página.
Si te gustó nuestro acertijo, puedes compartirlo en facebook o en twitter .
Y además quieres informarte de nuestras nuevas publicaciones, puedes seguirnos en nuestros perfiles en facebook, twitter, o por RSS
Vuelve a la primera parte
Regresa al Menú principal para ver más acertijos.


Matifutbol por Herminio López Arroyo se encuentra bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.



