

Un repartiment just

PRIMERA PART
 La Confederació Africana de Futbol ha decidit disputar un partit en benefici d'Haití. El partit tindrà lloc a l'estadi Soccer City de Johannesburgo. Per això, han convocat els millors futbolistes del continent.
La Confederació Africana de Futbol ha decidit disputar un partit en benefici d'Haití. El partit tindrà lloc a l'estadi Soccer City de Johannesburgo. Per això, han convocat els millors futbolistes del continent.
 per
per

Manquen poques hores per què comenci el partit. Samuel Eto'o i Didier Drogba han estat designats capitans dels equips vermell i blau, respectivament.


Ells són els que triaran els jugadors dels seus equips. I aquí és on es planteja el problema.
Per a efectuar el repartiment d'una manera més eficient, s'ordenen tots els jugadors per la seva qualitat, de major a menor.

Comença Eto'o triant el primer jugador (E), després tria Drogba (ED), després Eto'o (EDE), després Drogba (EDED), i així successivament...
Quan acaba la distribució, Drogba es queixa que la qualitat del seu equip és inferior a la de l'equip d'Eto'o, ja que a cada parella de jugadors elegits, el jugador triat per Eto'o és millor que el de Drogba: ED ED ED ED ED ED...

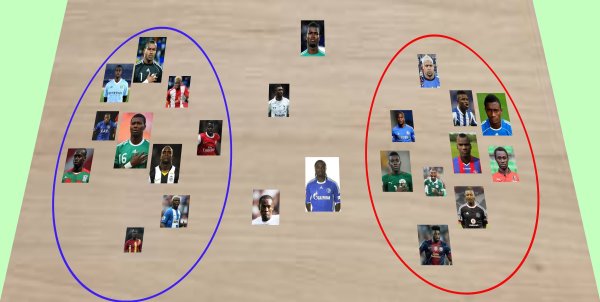
Per tant, decideixen fer un nou repartiment. Comença aquest cop triant Drogba (D), després tria Eto'o 2 jugadors (DEE), torna a triar Drogba 2 jugadors (DEEDD), i així fins al final.
Ara és Eto'o qui es queixa del repartiment, ja que si bé l'elecció està més equilibrada (DEED DEED DEED...), resulta que d'aquesta forma tots els porters disponibles han quedat enquadrats dins l'equip de Drogba, mentre que l'equip d'Eto'o no compta amb porters...
Sembla un problema irresoluble, sobretot quan a última hora es presenta un nou jugador, Boateng, de manera que ara n´hi ha un nombre imparell de jugadors per repartir entre els 2 equips!
¿Podries ajudar Eto'o i Drogba a repartir els jugadors de manera que ambdòs quedin satisfets?
Passa a la SEGONA PART per a conèixer la solució.

SEGONA PART
Dins de les diferents possibilitats de repartiment equitatiu, també podriem haver-hi pensat en aquesta altra: (DEED EDDE DEED EDDE DEED...) i en d'altres moltes combinacions que aparentment satisfan la necessitat d'igualtat entre els equips.
Però qualsevol solució d'aquest estil és només viable sempre que el salt de qualitat entre tots els jugadors sigui uniforme. A més, l'arribada de l'últim jugador desgavella completament qualsevol intent de repartiment semblant als descrit.
Amb un nombre senar de jugadors, el que podem fer és asignar una 'valoració' a cada jugador en funció de la seva qualitat. Sumem tots els punts, i escollim per cada equip jugadors que sumin la meitat d'aquesta xifra.
Aquest mètode també té els seus inconvenients:
Primer, perquè el total de punts serà divisible per 2 només en aproximadament la meitat de les ocasions (dependrà si otorguem punts de 0 a 10, d' 1 a 5, d' 1 a 100, etc).
En segon lloc, perquè l'assignació de punts a cada jugador s'haurà de fer d'una manera subjetiva, amb la qual no coincidiran necessàriament Eto'o i Drogba. Així, la igualtat dels dos equips segons la valoració d'una tercera persona pot no ser percebuda de la mateixa manera per aquests jugadors.
Tercer, porquè és possible que no hi hagi cap combinació de jugadors la suma de punts dels quals sigui exactament igual a la meitat dels punts totals obtinguts.
I en quart lloc, perquè tot i sent possible dividir-los en 2 equips amb igual puntuació, podrà passar que, com a l'exemple, tots els porters quedin enquadrats en un sol equip, o que un equip no tingui cap davanter, o que tots els jugadors d'un equip siguin esquerrans...
Així que, de quina forma podrem procedir per realitzar un repart que els resulti just a tots dos jugadors, Eto'o i Drogba?

En aquest cas aplicarem una fòrmula molt senzilla:
Encarregarem a qualsevol dels dos jugadors que realitzi el repartiment dels jugadors en dos equips, de la manera més equitativa possible, i sabent que serà l'altre jugador qui escollirà amb quin grup de jugadors es queda.
D'aquesta manera, el jugador que fa el repartiment quedarà satisfet, ja que sap que ha realitzat el repartiment de la forma més equitativa possible, ja que serà el contrari qui triarà en primer lloc el seu equip.
I el jugador que trïi també quedarà satisfet, ja que entre els dos grups n'haurà escollit el que pensa que té més qualitat dels 2.
Així que ara ja no hi ha cap impediment per disputar aquest interessant partit.
Aquest problema tracta d'un mètode molt efectiu per resoldre problemes de repartiments entre 2 persones que no són capaços d'arribar a un acord. Existeix també una variant d'aquest, en el cas que siguin 3 les persones entre les que hem de repartir un conjunt d'elements, una mica més difícil de posar en pràctica, però igualment efectiu:
Imaginem que Eto'o, Drogba i Boateng volen disputar un torneig triangular. En aquest cas, deixariem que Eto'o, per exemple, realitzés el repartiment dels jugadors en 3 equips: vermell, blau i groc.
Ara els donem a escollir a Drogba i a Boateng. Si cada un d'ells tria un equip diferent, Eto'o es quedaria amb el restant, i el tema estaria resolt.
Si Drogba i Boateng volen el mateix equip, suposem que l'equip vermell, llavors farem el sigüent: els hi donarem a escollir entre quedar-se'n amb l'equip groc o repartir-se'n entre ells els equips vermell i blau. Si només un d'ells escull l'equip groc, a l'altre li donarem el vermell (que era el que preferia inicialment), i Eto'o es quedarà amb el blau.
Si els dos jugadors prefereixen repartir-se'n entre ells els jugadors dels equips vermell i blau, només caldrà que segueixin el mètode descrit per 2 persones, i Eto'o es quedarà amb l'equip groc.
I si tots dos prefereixen l'equip groc abans que repartir-se'n el vermell i el blau, és perquè els dos jugadors perceben que l'equip groc té més qualitat que el blau (d'una altra manera haguessin preferit repartir entre ells els jugadors dels equips vermell i blau), pel qual en aquest cas haurem d'oferir-los a Drogba i a Boateng que es reparteixin entre ells els equips vermell i el groc de la forma descrita, i donarem l'equip blau a Eto'o.
Aquest és un exemple més del que coneixem per pensament lateral. Es tracta d'una forma d'abordar els problemes des d'un punt de vista diferent del que normalment utilitzem per enfrentar-nos amb ells, enfocant-los d'una forma indirecta i creativa.
Finalment, volem enviar des d'aquesta pàgina unes paraules de suport al poble d'Haití, esperant que articles como aquest serveixin, a més de per passar una bona estona i per aprendre quelcom de lògica matemàtica, perquè no ens oblidem tan aviat dels països que pateixen catàstrofes com la d'aquest país.
Si has arribat fins aquí, i desitges fer-nos qualsevol comentari sobre aquest tema, pots enviar-nos un correu amb el següent enllaç: contact@matifutbol.com . Agraïm enormement la teva col·laboració, ja que els teus comentaris són molt útils per poder millorar la nostra pàgina.
Si t'ha agradat la nostra endevinança, pots compartir-la al facebook o al twitter .
I si a més vols informar-te'n de les nostres noves publicacions, pots seguir-nos als nostres perfils al facebook, al twitter, o per RSS
Regressa a la primera part
Torna a la pàgina principal si vols veure més trencaclosques.


Matifutbol por Herminio López Arroyo se encuentra bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.



