

The problem of the fair division.

FIRST HALF
 The Confederation of African Football has decided to organize a benefit match for Haiti. The match will take place at the Soccer City Stadium in Johannesburg. They have invited the best players in the continent to play it.
The Confederation of African Football has decided to organize a benefit match for Haiti. The match will take place at the Soccer City Stadium in Johannesburg. They have invited the best players in the continent to play it.
 for
for

A few hours before the game starts, Samuel Eto'o and Didier Drogba have been designated captains of the red and the blue teams, respectively.


They're going to distribute the players in 2 teams. And then the problem comes up.
To make the distribution in a more efficient way, all players are ranked by their quality, from highest to lowest.

Eto'o picks the first player (E), then Drogba picks other player (ED), Eto'o picks again (EDE), then Drogba (EDED), and so on...
When the share-out ends, Drogba complains that the quality of his team is lower than Eto'o's team, since in each pair of players, the player chosen by Eto'o is better than Drogba's choice: ED ED ED ED ED ED...

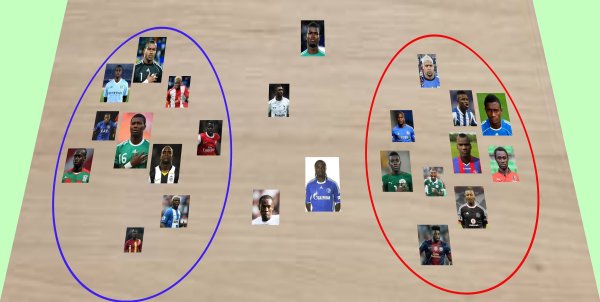
So they decide to make a new division. This time Drogba starts by choosing the first player (D), then Eto'o chooses 2 players (DEE), Drogba again chooses 2 players (DEEDD), and so on until the end of the list.
Now is Eto'o who complains of the distribution, since although the choice is more balanced (DEED DEED DEED...), he has the problem that all available goalkeepers have been assigned to Drogba's team, so that Eto'o's team has no goalkeepers...
It seems an unsolvable problem, especially when a new player, Boateng, comes a few minutes before the match starts, so that now there is an odd number of players to be divided among the 2 teams!
Could you help Eto'o and Drogba to split the players so that both will feel satisfied?
Go to the SECOND HALF to discover the solution

SECOND HALF
Among the different possibilities for an equitable distribution, we could also have thought of this one: (DEED EDDE DEED EDDE DEED...) and many other combinations that apparently would satisfy the need for equity between the teams.
But such solution is only viable as long as the quality gap between all the players is uniform. In addition, the arrival of the last player completely thwarts any attempt to sharing out through the methods described.
With an odd number of players, we can assign a 'value' to each player depending on his quality. We add up all the points, and we choose players for each team totalizing half of that figure.
This method also has its drawbacks:
First, because the total of points can be divided by 2 in only about half of the times (depending on if we issue points from 0 to 10, from 1 to 5, from 1 to 100, etc).
In second place, because the assignation of points to each player must be made subjetively, and it will not necessarily match with Eto'o and Drogba's thoughts. Thus, the equality of the 2 teams as assessed by a third party can not be perceived the same way by these players.
Third, it's possible that there's no combination of players whose sum of points is exactly equal to half the total points.
And fourth, because even being possible to divide them in 2 teams with the same score, it may occur that, as in the example, all the goalkeepers are assigned on the same team, or that a team has no defenders, or that all lefty players are on the same team...
So, how can we make a fair division for both players, Eto'o and Drogba?

In this case, we should apply a very simple method:
We order to either of the 2 players to undertake the distribution of the players in 2 teams, as equitably as possible, and knowing that the other player is who will choose first which one of the 2 groups he prefers to play with.
This way, the player who makes the deal will be satisfied, because he knows he has made the deal in the most equitable way as possible, knowing that the other player will be the first who chooses his team.
And the player who makes the election will be also satisfied, as he will choose the group he thinks that has a better quality among the 2.
So now there's no problem to play this interesting match.
This problem deals with a very effective method to solve distribution problems among 2 people who are unable to reach an agreement. There is also a variant of it, in case there are 3 persons among which we have to distribute a set of elements, a little harder to implement, but equally effective:
Imagine that Eto'o, Drogba and Boateng want to play a triangular tournament. In this case, we would let Eto'o, for instance, make the distribution of the players in 3 teams: red, blue and yellow.
Now we give Drogba and Boateng the chance to choose their teams. If each of them picks a different team, Eto'o would play with the remainder, and the problem would be resolved.
If Drogba and Boateng want the same team, let's assume it's the red one, then we do as follows: we give them a choice among picking the red team, or re-dividing the players of the red and the blue teams in another 2 new groups. If only one of them chooses the yellow team, the other will play with the reds (which was his initial choice), and Eto'o will stay with the blue team.
If both players prefer to re-divide the red and blue teams, they should simply follow the method described for 2 persons, and Eto'o will stay with the yellow team.
And if both prefer the yellow team rather than re-dividing the red and the blue teams, this means that the 2 players perceive that the yellow team has more quality than the blue one (otherwise they would have preferred to re-distribute the red and blue teams), so in this case we'll offer Drogba and Boateng to re-distribute the players of the red and the yellow teams as described, and we'll give Eto'o the blue team.
This is another example of what is called lateral thinking. It's a way to approach the problems from a different point of view from that we normally use to deal with, focussing them in a indirect and creative way.
Finally, we want to send from this page a word of support for the people from Haiti, hoping that articles like this will be also useful, in addition to having a good time and learning something of maths and logic, for not forgetting so soon these countries which suffer disasters such as Haiti.
If you arrived here, and want to tell us any comment on this topic, please send us an e-mail with the following link: contact@matifutbol.com . We greatly appreciate your help, as your comments are helpful to improve our site.
If you liked our riddle, you can share it in facebook or in twitter .
And if you want to be informed about our new publications, you can follow us in our facebook and twitter profiles, or by RSS.
Return to the first half
Go to the Home page to see more logic teasers.


Matifutbol por Herminio López Arroyo se encuentra bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.



