Eurobirthdays 2012
FIRST HALF
Michel Platini has decided to give each match, during the Euro Cup 2012 football championship organised by Poland and Ukraine, some commemorative medals to that line-up players of both teams whose birthdays are on the same day of the year.
For example, if in a match there are 2 first-team players (whether being of the same team or different teams) that cellebrate their birthday on February 23, UEFA will give them a medal each.
In the European Championship 2012 a total of 31 matches will be played, so that UEFA has estimated buying 10 medals will be enough for those players who fulfill that requirement. That is, they think this circumstance will occur during the championship in about 5 matches.
Do you think they'll have enough medals, the necessary number, or they will have to buy more?
Go to the second half to discover the solution
SECOND HALF
Probably your answer is similar to what intuitively and usually most people give: if we divide the 22 birthdays of the starting lineup players into the 365 days a year, we get a figure of 0.06027. That means birthdays of all the players account for only a 6,027% of the total days of the year.
So we expect a 6.027% probability that they match each other with their birthdays. Applying this percentage to the games in dispute, we have that 6% of 31 matches is equal to 1.87 matches. This means that in about 2 games weŽll have a couple of players that shares the same birthday, and therefore we'll need only 4 medals to give during the Euro Cup.
And as you might guess, the correct answer is far from what we regard as 'logical'. To solve the problem, first we should find out the probability of matching two players with birthdays on the same day in a football match. To do this, it will be easier to find out what is the probability that there isn't any pair of players with a birthday on the same day.
We start with 2 players. The second player can be born on any of the 364 days of the year not equal to the first player birth day. Therefore, the favorable cases are all year round except the birthday of the first person (364); and possible cases are every day of the year (365). Thus, the probability of not sharing birthdays will be:
Take a third player. Assuming that the first 2 players do not share their birthday, we have now 363 available days in which the third player can not match with the other 2 players: that is, a probability of 363/365 on the probability of 364/365 that the first 2 players do not coincide. That's a probability of:
We continue catching players. For the fourth one, the probability of mismatching with the other three will be of 362/365. And the joint probability of not matching the 4 players, is:
Following this procedure until the last of the 22 players who have entered the football pitch, the probability of not matching with the other 21 players is 343/365. And the probability of not mismatching all the players each other would be:
Surprisingly, the result is 52.43%. So, on the contrary, in a 47.57% of the matches, some player shall coincide with the same birthday as another, or what it is, in a 47.57% of the games we will stand the paradox that there is a couple of players whose birthdays are in the same day, contrary to what our intuition dictates.
And as 31 matches will be held in the European Championship, a 47.57% of 31 games equals to 14.75. So in about 15 matches we will see 2 starting line-up players who were born the same day of the year, so we will need so far than 30 medals for them.
Therefore, Michel Platini should visit quickly the jewelry to order more medals, as provided 10 medals are insufficient for all that he will have to give.
The fact is that we normally tend to imagine the probability that, starting from a particular player, there's another player who matches with his birthday's date (see image above). We think that 22 days (birthdays of 22 players) is a small fraction of the possible number of different days (365) to expect a repeat of the birthday. Hence, the probability with 22 players is underestimated (22/365).
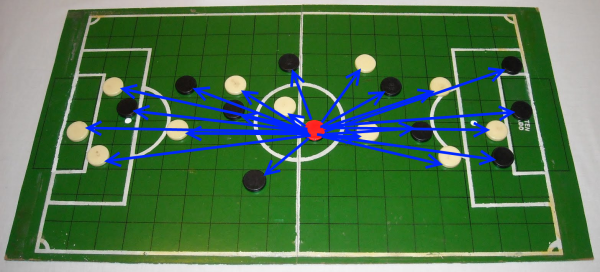
The key to understanding the subject is that there are many possible partners that can be formed as we increase the number of people in the group. Specifically, with 22 players we can form 231 different pairs of players (see image above). That way the probability turns out to be so high in such a small group, when this group is thought in terms of the number of possible pairs, rather than as the number of individuals.
This way, and applying the formulas described later on, we obtain for the 22 lineup players ( n = 22 ) a probability of 0.475695 (a 47.57%).
Adding the referee ( n = 23 ) we've got a 50%, a chance of 50.73% to be exact.
With the 2 linesmen ( n = 25 ) the probability amounts to 56.87%.
And it we add the 12 reserves of each team, the 2 assistant judges, and the fourth official ( n = 52 ) we reach a probability of 97.80%. A 97.80% with only 51 people!
This subject is known as the 'birthday paradox', which states that, if there are 23 people in a room, there is a 50.73% probability of 2 people having the same birthday, and for 57 or more people the chance is greater than 99%.
In fact, this is not a paradox, since it doesn't involve a logical contradiction; it's a paradox in the sense that mathematical reality contradicts intuition. Many people think that the probability is much lower, and that it takes many more people to reach a 50% probability.
Finally, note that throughout this process we have overlooked about those born on a February 29th (leap years). But,
we have also overlooked the possibility that some national team having twin brothers, or that coaches are not conditioned for the delivery of the medals in order to get some players rather than others, or that all dates are equiprobable, ie, the distribution of the birthdays is uniform throughout the year.
However, as shown at the table on the right side, there are dates when birthdays concentrate, and dates in which almost no one is born, so the probabilities that two people share their birthday are greater than 1/365. So, we would still have to buy more medals!
In mathematical terms, we can study all these problem like: for n people:
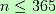
We have the probability p about not sharing birthdays, obtained by the following formula:
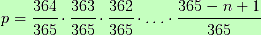
If we use factorials, we have the following expression:
Since this is the probability that there's no pair of people whose birthdays match, the probability that at least a couple of people celebrate the birthday on the same day is:
Once Euro 2012 has ended, we can count how many medals would have been deliverd. Let's see which birthday matches took place in the starting lineups:
Pol - Gre: Wasilewski & Papastatopoulos (Jun 9)
Ita - Cro: Bonucci & Srna (May 1)
Cro - Spa: Pleticosa & Silva (Jan 8)
Ukr - Fra: Khacheridi & Debuchy (Jul 28), Tymoshchuk & Mexes (Mar 30), Shevchenko & Konoplyanka (Sep 9)
Ukr - Sue: Shevchenko & Konoplyanka (Sep 9), Isaksson & Ibrahimovic (Oct 3)
Swe - Fra: Isaksson & Ibrahimovic (Oct 3), Bajrami y Ben Arfa (Jul 3)
Swe - Eng: Isaksson & Ibrahimovic (Oct 3)
Eng - Ukr: Hart & Garmash (Apr 19)
Por - Spa: Veloso & Iniesta (May 11)
Ger - Gre: Klose & Papastathopoulos (Jun 9)
As you can see, 28 medals should have been delivered, only 2 less than we had calculated!
If you arrived here, and want to tell us any comment on this topic, please send us an e-mail with the following link: contact@matifutbol.com . We greatly appreciate your help, as your comments are helpful to improve our site.
If you liked our riddle, you can share it in facebook or in twitter .
And if you want to be informed about our new publications, you can follow us in our facebook and twitter profiles.
Return to the first half
Go to the Championship to see more logic teasers.
Matifutbol by Herminio López Arroyo is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.